موضوع تعبير عن مساحة المعين

موضوع تعبير عن مساحة المعين، في الهندسة الإقليدية الطائرة، يكون المعين رباعي الأضلاع، وجميع جوانبه الأربعة لها نفس الطول.
هناك اسم آخر للمعين، وهو رباعي الأضلاع أو متوازي الأضلاع، لأن متوازي الأضلاع يعني أن جميع أضلاعه متساوية في الطول.
فما هو المضلع؟ وكيف يمكن الحصول على مساحته ومحيطه؟ تابع موقع مقال للتعرف على موضوع تعبير عن مساحة المعين.
محتويات المقال
ما هو المعين؟
في الواقع، المعين عبارة عن شكل رباعي الأوجه، حيث يكون كل جانب بنفس الطول، وكل زوج متعاكس من الزوايا متساوي.
وتظهر المعينات في كل شيء من الطائرات الورقية إلى بلاط الأرضيات، واعتمادًا على المعلومات، التي لديك حول المعين المعني، ويمكنك حساب مساحة المعين بالطرق التالية.
جاءت كلمة “المعين” من الكلمة اليونانية ῥόμβος، وهذا يعني شيئًا يدور، وتم استخدام الكلمة من قبل إقليدس وأرخميدس.
وهو الذي استخدم مصطلح “المعين الصلب” لـ bicone، وهما مخروطان دائريان يتقاسمان قاعدة مشتركة.
كما أن السطح الذي نشير إليه باسم المعين اليوم هو مقطع عرضي من bicone، على مستوى من خلال قمم المخروطين.
شاهد أيضًا: مساحة المربع وطول القطر
ما هي الخصائص الأساسية للمعين؟
يحتوي كل معين على قطرين يربطان أزواجًا من القمم المعاكسة، وزوجين من الجوانب المتوازية، باستخدام المثلثات المتطابقة.
يمكن للمرء أن يثبت أن المعين متماثل عبر كل من هذه الأقطار، ويترتب على ذلك أن أي معين له الخصائص التالية:
- الزوايا المقابلة من المعين لها نفس القدر.
- قطري المعين متعامدين، بمعنى أن المعين رباعي الأضلاع.
- تتقاطع أقطاره مع الزوايا المتقابلة.
تشير الخاصية الأولى إلى أن كل معين هو متوازي الأضلاع، وبالتالي فإن المعين يحتوي على جميع خصائص متوازي الأضلاع:
على سبيل المثال، الجوانب المقابلة متوازية؛ الزوايا المجاورة مكملة، القطران يشطران بعضهما البعض، أي خط عبر نقطة المنتصف يقسم المنطقة.
ومجموع مربعات الأضلاع يساوي مجموع مربعات الأقطار (قانون متوازي الأضلاع).
وبالتالي تدل على الجانب المشترك، باعتباره a والأقطار هي p و q في كل معين:
![]()
ليس كل متوازي أضلاع معين، على الرغم من أن أي متوازي الأضلاع بأقطار متعامدة (الخاصية الثانية) هو معين.
وبشكل عام، أي رباعي أضلاع أضلاعه متعامدة، أحدها خط التماثل، فهو طائرة ورقية، وكل معين هو طائرة ورقية.
وأي رباعي أضلاع على شكل طائرة ورقية وأي متوازي أضلاع فهو معين، كما أن المعين رباعي عرضي، أي أنه يحتوي على دائرة منقوشة مماسة للجوانب الأربعة.
متى يكون الشكل الرباعي البسيط ميعن؟
الرباعي البسيط (غير المتقاطع مع الذات) هو المعين إذا وفقط إذا كان أيًا مما يلي:
- متوازي الأضلاع، حيث ينقسم قطري إلى زاوية داخلية.
- كما أن متوازي الأضلاع حيث يتساوى طول جانبين متتاليين على الأقل.
- متوازي الأضلاع، حيث تكون الأقطار متعامدة (متوازي الأضلاع).
- كذلك رباعي الأضلاع بأربعة جوانب متساوية الطول (بحكم التعريف).
- رباعي الأضلاع، حيث تكون الأقطار متعامدة وتتقاطع مع بعضها البعض.
- ولذلك رباعي الأضلاع، حيث يقسم كل قطري زاويتين داخليتين متقابلتين.
- ABCD رباعي الأضلاع يمتلك نقطة P في مستواه، بحيث تتطابق المثلثات الأربعة ABP وBCP وCDP وDAP.
- ABCD رباعي الأضلاع حيث يكون للمحاور في المثلثات ABC وBCD وCDA وDAB نقطة مشتركة.
كيف يمكن التعبير عن الأقطار في المعين؟
يمكن التعبير عن طول الأقطار p = AC و q = BD، من حيث جانب المعين a وزاوية قمة واحدة α كالتالي:
![]() ،
، ![]()
وهذه الصيغ هي نتيجة مباشرة لقانون جيب التمام.
ما هو الـ inradius وكيف يمكن التعبير عنه في المعين؟
الـ inradius هو عبارة عن نصف قطر دائرة منقوشة في المعين، يرمز لها بـ r، ويمكن التعبير عنه من حيث الأقطار p و q كالآتي:
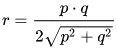
أو من حيث طول الضلع a وأي زاوية قمة α أو β مثل:
![]()
كيف يمكن حساب مساحة المعين؟
يمكن حساب مساحة المعين من خلال الطرق المختلفة الآتية، وهي:
الطريقة الأولى
ضرب ارتفاع المعين في طول أحد أضلاعه، حيث أن الارتفاع هو المسافة بين أي جانبين متقابلين من المعين.
مثال: إذا كان ارتفاع معينًا ما هو 8 بوصات، وكان طول ضلع هذا المعين هو 10 بوصات، فما هي مساحة هذا المعين؟
الحل: مساحة المعين = ارتفاع المعين × طول أحد أضلاعه، وبالتالي فإن مساحة المعين = 8 × 10 = 80 بوصة مربعة، وهي مساحة هذا المعين.
تابع أيضًا: مساحة شبه المنحرف متساوي الساقين والقائم
الطريقة الثانية
قم بتربيع طول أي جانب، واضرب الناتج في جيب إحدى الزوايا داخل الماس، ويمكن تحديد جيب الزاوية باستخدام حاسبة علمية أو من قائمة جيب الزاوية للزوايا المشتركة.
مثال: إذا كان للمعين جانب طوله 6 بوصات، وكانت إحدى زواياه هي 30 درجة مع جيب تمام يساوي 0.5، فما هي مساحة هذا المعين؟
الحل: طول مربع الجانب هو 6، ولإيجاد المساحة لا بد من تربيع جانب المعين، وبالتالي فإن تربيع الجانب = 6 × 6 = 36.
والآن نأتي للخطوة التالية، وهي ضرب تربيع الجانب في جيب الزاوية 30، وبالتالي سنحصل على مساحة المعين، أي أن مساحة المعين = 36 × 0.5 = 18 بوصة مربعة، وهي مساحة هذا المعين.
ما هي الخصائص المزدوجة بين المعين والمستطيل؟
المضلع المزدوج للمعين هو المستطيل:
- يشتمل المعين على جميع الجوانب متساوية، في حين أن المستطيل له جميع الزوايا متساوية.
- المعين له زوايا متساوية، بينما المستطيل له أضلاع متساوية.
- يحتوي المعين على دائرة منقوشة، في حين أن المستطيل له دائرة محيطية.
- يحتوي المعين على محور التماثل من خلال كل زوج من زوايا القمة المتقابلة، بينما يحتوي المستطيل على محور.
- التماثل من خلال كل زوج من الجوانب المتقابلة.
- تتقاطع أقطار المعين عند زوايا متساوية، بينما تكون أقطار المستطيل متساوية في الطول.
- الشكل الذي شكله ربط نقاط المنتصف لجوانب المعين مستطيل، والعكس صحيح.
كيف يمكن حساب محيط المعين؟
يحتوي المعين على أربعة جوانب بنفس الطول، ولكن على عكس جوانب المربع، لا يجب أن تتقاطع جوانب المعين بزوايا 90 درجة، محيط أي جسم ثنائي الأبعاد مغلق هو المسافة المحيطة به من الخارج.
وبالتالي فإن حساب محيط المعين يعد أمرًا بسيطًا، نظرًا لجوانبه أو أضلاعه المتساوية في الطول.
حيث يتم حساب محيط المعين من خلال ضرب طول أحد أضلاعه أو جوانبه في 4، حيث أن الرقم 4 هو عدد أضلاعه.
مثال: إذا كان طول أحد جوانب معين يساوي 45 سم، فما هو محيط هذا المعين؟
الحل: بتطبيق القانون نجد أن محيط المعين = 45 × 4 = 180 سم مربع.
معادلة ديكارتية
تتكون جوانب المعين المتمركزة في الأصل، مع وجود أقطار يسقط كل منها على محور، من جميع النقاط (x ،y) مرضية
![]()
خصائص أخرى
- واحدة من خمسة أنواع شعرية ثنائية الأبعاد هي الشبكة المعينية، وتسمى أيضًا شعرية مستطيلة الشكل.
- يستطيع المعين المتطابق تجانب الطائرة ثنائية الأبعاد بثلاث طرق مختلفة، بما في ذلك، المعين 60 درجة، وبلاط المعين.
- النظائر ثلاثية الأبعاد للمعين تشمل الـ bipyramid والـ bicone.
- العديد من الوجوه المتعددة لها وجوه معينية، مثل الاثني عشر المعياري والاثني عشر شبه المنحرف.
قد يهمك: معلومات عن مساحة المستطيل
في النهاية، نرجو أن تكونوا قد استفدتم من هذا المحتوى الهادف، وتعلمتم كيفية الحصول على كل من مساحة المعين ومحيطه بكل سهولة، وإذا أردتم المزيد، تابعونا على موقع مقال.