تحليل الاعداد الى عواملها الاولية
تحليل الاعداد الى عواملها الاولية، يمكن تعريف الأعداد الأولية بأنها الأعداد الصحيحة التي اكبر من رقم واحد.
كما أن الأعداد الأولية لا تقبل القسمة إلا على الواحد أو على نفسها، من هذه الأعداد الأولية: 2، 3، 5، 7، 11، 13، 17، 19، 23.
وبالتالي قد يرى البعض منا صعوبة في عملية تحليل الأعداد إلى عواملها الأولية، ولهذا الأمر خصيصًا يمكنك التعرف على الطريقة الصحيحة للتحليل من خلال موقع مقال maqall.net
محتويات المقال
تحليل الاعداد الى عواملها الاولية
- يحتاج الكثير منا إلى معرفة الطريقة الصحيحة لـ تحليل الاعداد الى عواملها الاولية
- حيث يجد البعض صعوبة في التحليل، ومن التفاصيل والمعلومات الهامة في عملية التحليل:
- تمتلك الأعداد الأولية عاملين فقط، وهما: العدد نفسه، والعدد واحد.
- وبهذا الشكل لا يمكنها أن تتعامل إلا مع هذان العاملين فقط لا غير
- قد يساوي حاصل ضرب الأعداد الأولية بعضها البعض، وفي هذه العملية يتم تجاهل رقم 1، حيث أنه لا يعتبر من الأعداد الأولية.
- كما يجب أن يذكر بأن الأعداد التي تنتج من حاصل ضرب الأعداد الصحيحة تسمى بالأعداد المركبة، والأعداد الصحيحة
- التي تضرب ببعضها البعض من أجل الحصول على أعداد مركبة يطلق عليها العوامل، قد تكون هناك عوامل أولية أو غير أولية.
شاهد أيضًا: هل تمكن موزلي من تطوير الجدول الدوري حسب الاعداد الكتلية أم لا
طرق تحليل الأعداد الأولية
- يمكنك أن تتعرف على الطريقة الصحيحة لتحليل الأعداد الأولية.
- وهذا يتم من خلال عدة طرق مختلفة، توجد الطريقة التقليدية وطريقة الشجرة
وللمزيد من التفاصيل حول هذه الطرق:
الطريقة التقليدية
- في هذه الطريقة يتم قسمة العدد على أصغر عدد أولي ممكن، ومن بعدها يتم القسمة على عدد أخر، وفي النهاية يمكنك أن تصل إلى عدد أولي جديد.
والطريقة كالاتي:
- السؤال: قم بتحليل العدد 12 إلى عوامله الأولية.
- الإجابة: القسمة على عدد أولي وهو العدد 2، لأن 12 عدد زوجي، وذلك كما يلي: 12/2=6، واعتبار العدد (2) أول عدد أولي لعدد (12).
- يعتبر العدد 6 ليس عدد أولي، لذا يجب أن يتم القسمة على أصغر عدد أولي وهو العدد 2، وهذا يرجع إلى أن العدد 6 هو عدد زوجي
- وذلك حسب الآتي: 6/2=3، وهو عدد أولي، لذلك يجب التوقف هنا، واعتبار العددين 2،3 أعداداً أولية للعدد 12.
- الأعداد الأولية الخاصة بالعدد 12 تكون على هذا النحو: 2×2×3 = 12.
يمكنك تمثيل العملية السابقة من خلال الجدول التالي:
| 12÷ | 2 |
| 6÷ | 2 |
| 3÷ | 3 |
| 1 | – |
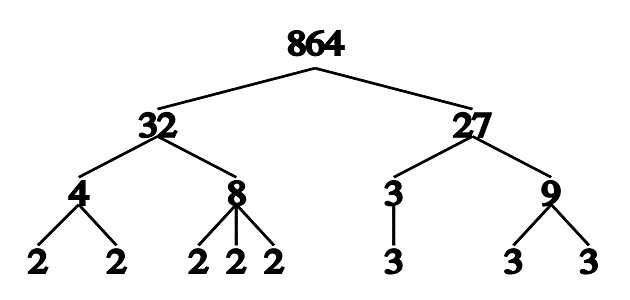
طريقة الشجرة
- تعد طريقة حديثة من أجل سهولة تحليل الأعداد الأولية، حيث انك من خلال هذه الطريقة.
- تتمكن من عمل مخطط لتجزئة الأعداد وبالتالي تصل إلى عواملها الأولية
- تعتبر من الطرق البسيطة والتي قد تساعد الشخص على تعلم الطريقة الصحيحة لتحليل الأعداد بشكل سهل في بداية الأمر، والمثال التالي يوضح لك هذه الطريقة:
- السؤال: قم بتحليل العدد 24 إلى عوامله الأولية.
- الإجابة: نعثر أولًا على عددين حاصل ضربهما هو 24، وهما (2×12) مثلاً.
- بما أن العدد 12 هو عدد غير أولي، إذا يجب العثور على عددين حاصل ضربهما هو 12، وهما (3×4) مثلاً.
- لكن العدد 4 هو عدد غير أولي، في هذه الحالة يجب العثور على عددين حاصل ضربهما هو 4، وهما (2×2)، وبالتالي هم عددان أوليان.
- إذا فإن الأعداد الأولية للعدد 24 هي: 3×2×2×2 = 24.
- يمكننا أن نقوم بتمثيل ما سبق على هذا النحو: 24 ← 2×12 ← 2×3×4 ← 2×3×2×2.
تابع أيضًا: بحث عن المجموعة الشمسية للصف الاول الاعدادي
أمثلة تحليل الأعداد إلى عواملها الأولية
- يمكنك أن تتعرف على طريقة تحليل الاعداد الى عواملها الاولية، حيث أنها سوف تساعدك في إجراء الكثير من الحسابات المختلفة بسهولة كبيرة.
- كل ما عليك هو أن تتابع طريقة الحل بشكل دقيق وبتركيز شديد
- وبعدها سوف تتمكن من تطبيق الطريقة على أي مسألة أخرى، ومن هذه الأمثلة هي:
المثال الأول
- السؤال: حلل العدد 36 إلى عوامله الأولية.
- الحل: القسمة على عدد أولي، هو العدد 2، وذلك كما يلي: 36/2 = 18، يعتبر العدد 2 هو أول عدد أولي لعدد 36.
- أما العدد 18 لا يعتبر عدد أولي، لذا لا يمكن استخدامه، ولكن العدد 2 أولي، وذلك كما يلي: 18/2=9، واعتبار (2) ثاني عامل أولي لعدد 36.
- يُعد العدد 9 ليس عدد أولي أيضًا، لذا يجب قسمته على عدد أخر وهو العدد 3، وذلك كما يلي: 9/3=3، واعتبار (3) ثالث عامل أولي لعدد 36.
- يعتبر العدد 3 هو العدد الأولي، لذلك يرجى التوقف هنا، اعتبار أن العدد 3 رابع عامل أولي لعدد 36.
- الأعداد الأولية للعدد 36 تكون على النحو الآتي: 2×2×3×3 = 36.
المثال الثاني
- السؤال: حلل العدد التالي إلى عوامله الأولية : 1386.
- الحل: يتم العثور على عددين حاصل ضربهما هو 1368، وهما (2×684) مثلاً.
- العدد 684 يعتبر عدد غير أولي، وبالتالي يجب العثور على عددين حاصل ضربهما هو 684، وهما (171×4) مثلاً.
- يعد العدد 4 والعدد 171 إعداد غير أولية، وبالتالي يجب الحصول على عددين حاصل ضربهما 4، عددين أيضًا حاصل ضربهما هو 171، وهما: (2×2)، و57×3 على الترتيب.
- العدد 57 هو عدد غير أولي، لذا يجب العثور على عددين حاصل ضربهما هو 57، وهما (3×19) مثلاً، وكلاهما عدد أولي، لذا سوف نتوقف هنا.
- بالتالي فإن الأعداد الأولية للعدد 1368 هي: 2×2×2×3×3×19 = 1386.
- 1386 ← 2×684 ← 2×171×4 ← 2×57×3×2×2 ← 2×19×3×3×2×2.
المثال الثالث
- السؤال: حدد العدد 90 إلى عوامله الأولية.
- الحل: يجب أن نعثر على عددين حاصل ضربهما هو: 90، وهما (3×30) مثلاً.
- إذا العدد 30 لا يعتبر عدد أولي، وبالتالي يجب الحصول على عددين حاصل ضربهما هو 30، وهما (15×2) مثلاً.
- العدد 15 غير أولي ولكن العدد 2 أولي، إذا يجب البحث عن عددين حاصل ضربهما هو 15، وهما (5×3)، وكلاهما أوليين لذا يجب التوقف هنا.
- إذا فإن الأعداد الأولية للعدد 90 هي: 2×3×3×5= 90.
- 90 ← 3×30 ← 3×2×15 ← 2×3×5×3.
اقرأ أيضًا: ما هي الاعداد النسبية في الرياضيات؟
المثال الرابع
- السؤال: حلل العدد 30 إلى عوامله الأولية.
- الحل: قم بالقسمة على أصغر عدد أولي، وهو العدد رقم 2، لان العدد 30 يعد من الأعداد الزوجية، وذلك كما يلي: 30/2 = 15، واعتبار (2) أول عامل أولي لعدد 30.
- يعتبر العدد 15 ليس عدد أولي، لذا يجب البحث عن عددين حاصل ضربهما هو 15، وذلك كما يلي: 15/3=5، وهو عدد أولي، واعتبار (3) ثاني عامل أولي لعدد 30.
- يعد العدد 5 هو عدد أولي، لذا يجب التوقف هنا واعتبار (5) ثالث عامل أولي لعدد 30.
- إذا تكون الأعداد الأولية للعدد 30 تكون على النحو الآتي: 2×3×5 = 30.
بهذا الشكل نكون قد تعرفنا على الطريقة الصحيحة لـ تحليل الاعداد الى عواملها الاولية.
تعد عملية تحليل الأعداد من العمليات البسيطة والسهلة التي لا تحتاج إلى المزيد من التفكير.
ولكنها تحتاج منك بعض التركيز ومعرفة القواعد الخاصة بالتحليل ومعرفة الأرقام الأولية بشكل جيد.
وبعدها يمكنك أن تنظر إلى عدة أمثلة من أجل تثبيت طريقة التطبيق، وتطبيقها بعد ذلك في أي وقت من الأوقات على أي رقم.