ترتيب العمليات الحسابية حسب الأولوية
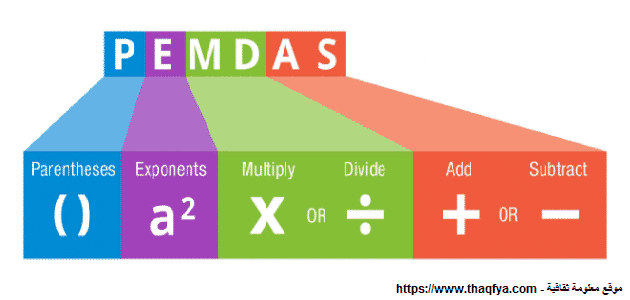
ترتيب العمليات الحسابية حسب الأولوية، يشير ترتيب العمليات الحسابية إلى ترتيب العمليات التي هي عبارة: عن القسمة والضرب والجمع والطرح والأقواس والأس، والتي يتم استخدامها في الرياضيات والعلوم والتكنولوجيا، والعديد من لغات برمجة الكمبيوتر.
وسنتحدث اليوم في مقالنا هذا عن كيفية ترتيب هذه العمليات مع ذكر بعض الأمثلة، لذا، تابعوا موقع مقال للتعرف على ترتيب العمليات الحسابية حسب الأولوية.
محتويات المقال
ترتيب العمليات الحسابية
يكون ترتيب هذه العمليات على النحو التالي:
- فك الأقواس
- الأس واستخراج الجذر.
- الضرب والقسمة.
- الجمع والطرح.
هذا يعني أنه في حالة ظهور تعبير فرعي بين عاملين في تعبير رياضي، يجب تطبيق العامل الأعلى في القائمة أعلاه أولاً.
هذا وتسمح القوانين التبادلية والترابطية للجمع والضرب بإضافة مصطلحات بأي ترتيب، وعوامل الضرب بأي ترتيب، ولكن العمليات المختلطة، يجب أن تخضع للترتيب القياسي للعمليات.
شاهد أيضًا: العصف الذهني في الرياضيات PDF
استبدال العمليات الحسابية
في بعض السياقات، من المفيد استبدال القسمة بالضرب بالمقلوب (معكوس الضرب)، والطرح بجمع المقابل، (المعكوس الجمعي).
على سبيل المثال، في جبر الكمبيوتر، يتيح ذلك للفرد التعامل مع عدد أقل من العمليات الثنائية، ويجعل من السهل استخدام التبديل.
والترابط عند تبسيط التعبيرات الكبيرة، هكذا: 3 ÷ 4 = 3 ×1/4، بمعنى آخر: حاصل قسمة 3 على 4 يساوي، حاصل ضرب 3 في 1/4
أيضًا يمكن القول أن “4 – 3 = (4-) + 3″، وبمعنى آخر، الفرق بين 3 و4 يساوي مجموع 3 و 4-.
وبالتالي، يمكن اعتبار “7 + 3 – 1” هو مجموع “7 + (3-) + 1″، ويمكن إضافة المجموعات الثلاثة، بأي ترتيب في جميع الحالات مع إعطاء “5” كنتيجة.
السبب في استخدام الأقواس
يتم تمديد رمز الجذر √ بشكل تقليدي بواسطة شريط (يسمى vinculum) فوق الجذر، وهذا يتجنب الحاجة إلى وجود أقواس حول الجذر.
وتستخدم الدوال الأخرى الأقواس حول الإدخال لتجنب الغموض، ويمكن حذف الأقواس، إذا كان الإدخال متغيرًا رقميًا واحدًا أو ثابتًا كما في حالة (sin (x.
فمن الممكن كتابتها sin x (بدون أقواس)، ومن الاصطلاحات المختصرة الأخرى المستخدمة أحيانًا، عندما يكون الإدخال أحاديًا.
وبالتالي، فإن (sin 3x = sin (3x أفضل من sin (x)) 3)، لكن sin x + y = sin (x) + y، لأن x + y ليست أحادية الحد.
ومع ذلك، هذا يعد غامضًا، وغير مفهوم عالميًا خارج سياقات محددة، كما تتطلب بعض الآلات الحاسبة، ولغات البرمجة أقواسًا حول مدخلات الوظيفة، والبعض الآخر لا يتطلب ذلك.
يمكن استخدام رموز التجميع لتجاوز الترتيب المعتاد للعمليات، ويمكن التعامل مع الرموز المجمعة كتعبير واحد.
أيضًا يمكن إزالة رموز التجميع باستخدام قوانين الترابط والتوزيع، كما يمكن إزالتها إذا كان التعبير الموجود داخل رمز التجميع مبسطًا بدرجة كافية، بحيث لا ينتج عن إزالتها أي غموض.
فن استذكار العمليات الحسابية
غالبًا ما يستخدم فن الاستذكار لمساعدة الطلاب على تذكر القواعد، بما في ذلك الأحرف الأولى من الكلمات، التي تمثل عمليات مختلفة، ويتم استخدام فن الاستذكار في بلدان مختلفة.
لكن، قد يكون فن الاستذكار هذا مضلل عند كتابته بهذه الطريقة، على سبيل المثال، قد يؤدي سوء تفسير أي من القواعد المذكورة أعلاه على أنها تعني “الإضافة أولاً، ثم الطرح بعد ذلك” إلى تقييم التعبير بشكل غير صحيح.
![]()
عند تقييم التعبير أعلاه، يجب إجراء عمليات الجمع والطرح، بالتتابع من اليسار إلى اليمين، لأن الطرح مترابط بين اليسار، ويعتبر عملية غير ارتباطية.
إما العمل من اليسار إلى اليمين، أو التعامل مع الطرح، على أنه إضافة رقم موقّع سينتج الإجابة الصحيحة.
سيؤدي إجراء عملية الطرح بترتيب خاطئ إلى الإجابة غير الصحيحة، لا تعكس فن الاستذكار تجميع الجمع / الطرح أو الضرب / القسمة.
لذا فإن استخدامها قد يؤدي إلى سوء الفهم هذا، يوجد غموض مشابه في حالة التقسيم التسلسلي، على سبيل المثال، يمكن قراءة التعبير ” a ÷ b ÷ c × d ” بطرق متعددة، ولكنها قد لا تصل دائمًا إلى نفس الإجابة.
![]()
يعتبر التقسيم تقليديًا بمثابة جمعيات يسارية، بمعنى، إذا كان هناك عدة أقسام متتالية، فإن ترتيب الحساب ينتقل من اليسار إلى اليمين:
![]()
علاوة على ذلك، فإن العادة الرياضية المتمثلة في الجمع بين العوامل، وتمثيل القسمة كضرب بمقلوب تقلل بشكل كبير من تكرار الانقسام الغامض.
![]()
حالة تسلسل الأس
إذا تمت الإشارة إلى الأس بواسطة رموز مكدسة باستخدام الترميز المرتفع، فإن القاعدة المعتادة، هي العمل من أعلى إلى أسفل:
![]() والتي لا تساوي عادةً ab)c).
والتي لا تساوي عادةً ab)c).
ومع ذلك، عند استخدام تدوين عامل التشغيل مع علامة الإقحام (^) أو السهم (↑)، لا يوجد معيار مشترك.
على سبيل المثال، يقوم مايكروسوفت إكسيل، ولغة البرمجة الحسابية MATLAB، بتقييم ” a ^ b ^ c ” كـ ” ab) c) “.
لكن بحث جوجل و Wolfram Alpha يكون التدوين كـ ” (a (bc “، وهكذا فإن 2 ^ 3 ^ 4، يتم تقييمها بـ 4,096 في الحالة الأولى، ويكون تقييمها 262,144 في الحالة الثانية.
علامة الطرح الأحادية
هناك اصطلاحات مختلفة بخصوص العامل الأحادي – (عادة ما تقرأ “ناقص”، وفي الرياضيات المكتوبة أو المطبوعة، يتم تفسير التعبير ” 32– ” على أنه يعني ” (32) – 0 = 9- “.
في بعض التطبيقات ولغات البرمجة، لا سيما مايكروسوفت إكسيل، (وتطبيقات جداول البيانات الأخرى).
ولغة البرمجة bc، يكون للمشغلين الأحاديين أولوية أعلى من العوامل الثنائية، أي أن السالب الأحادي له أسبقية أعلى من الأُس.
لذلك في تلك اللغات ” 32– ” سيتم تفسيره على أنه ” 2(3-) = 9 “، وهذا لا ينطبق على ثنائي ناقص عامل الناقص.
تابع أيضًا: ما هي الاعداد النسبية في الرياضيات؟
الخلط بين القسمة والضرب
وبالمثل، يمكن أن يكون هناك غموض في استخدام رمز الشرطة المائلة، في تعبيرات مثل ” 1/2x “.
إذا أعاد أحد كتابة هذا التعبير كـ ” 1 على 2x ” ثم فسر رمز القسمة، على أنه يشير إلى الضرب بالمقلوب، يصبح هذا:
![]()
بهذا التفسير فإن ” 1 على 2x ” يساوي ” (2 ÷ 1) مضروب في x “، ومع ذلك، في بعض الأدبيات الأكاديمية.
يتم تفسير الضرب الذي يُشار إليه بالتجاور (المعروف أيضًا باسم الضرب الضمني)، على أنه ذو أسبقية أعلى من القسمة.
وتنص تعليمات تقديم المخطوطات لمجلات Physical Review، على أن الضرب له أسبقية أعلى من القسمة بشرطة مائلة.
وهذا أيضًا هو العرف الذي لوحظ في كتب الفيزياء المدرسية البارزة، مثل Course of Theoretical Physics.
ذلك بواسطة Landau وLifshitz ومحاضرات فاينمان في الفيزياء.
أمثلة على ترتيب العمليات الحسابية
بسّط المقدار: 5 ÷ 2(3 – 8) 3 – 16
الحل: يجب أن تتذكر أنه يجب تبسيط ما بداخل الأقواس قبل أن تقوم بإجراء عملية التربيع، لأن 2(3 – 8) تختلف عن 32 – 82.
ويمكن وصف ذلك كالتالي:
5 ÷ 2(3 – 8) 3 – 16
كما أن 5 ÷ 2(5) 3 – 16 =
5 ÷ (25) 3 – 16 =
كذلك 5 ÷ 75 – 16 =
وأخيرًا يساوي 15 – 16 =
1 =
وبهذا تكون القيمة المبسطة للمقدار هي 1
بسّط المقدار: 2 ÷ [(3 – 6) 2 – 4] 3 – 4
الحل: سنقوم بتبسيط المقدار من الداخل إلى الخارج: أولاً، الأقواس، ثم الأقواس المربعة، مع الحرص على تذكر أن علامة “الطرح”.
فعلى 3 أمام الأقواس تتوافق مع 3، فقط بمجرد الانتهاء من تجميع الأجزاء، سنقوم بعملية القسمة، متبوعة بجمع العدد 4.
ويمكن وصف ذلك كالتالي:
2 ÷ [(3 – 6) 2 – 4] 3 – 4
2 ÷ [(3) 2 – 4] 3 – 4 =
كما أن 2 ÷ [6 – 4] 3 – 4 =
2 ÷ [2-] 3 – 4 =
كذلك 2 ÷ 6 + 4 =
أيضًا 3 + 4 =
7 =
إذن قيمة المقدار المبسطة هي 7
بسّط المقدار: (1 – 4) + 5 / 2(2 + 1) + (2 – 3)
الحل: هذا يعمل تمامًا مثل الأمثلة السابقة؛ عليك فقط أن تعامل البسط منفصلاً عن المقام، حتى تحصل على جزء يمكنك (ربما) تبسيطه، ويمكن وصف ذلك كالتالي:
(1 – 4) + 5 / 2(2 + 1) + (2 – 3)
(3) + 5 / 2(3) + (1) =
8 / 9 + 1 =
8 / 10 =
4 / 5 =
وبهذا تكون القيمة المبسطة للمقدار هي 4 / 5
اخترنا لك: معنى الجبر في الرياضيات
كانت هذه نبذة عن ترتيب العمليات الحسابية حسب الأولوية، نرجو أن تكونوا على علم وافٍ بترتيب العمليات الحسابية الآن، كما يمكنكم أرشفة هذا المقال واستخدامه وقت الحاجة .. وللمزيد من المواضيع الرياضية الأخرى، زوروا موقع مقال!