حساب حجم المخروط الدوراني بالتكامل

حساب حجم المخروط الدوراني بالتكامل، موقع مقال mqaall-com يقدم لكم حساب حجم المخروط الدوراني بالتكامل، حيث مفهوم المخروط (Cone) أنه مجسَّم لديه قاعدة واحدة فقط، وهي مُسطحة الشكل ودائرية، ولديه نقطة مدببة موقعها أعلاه، وتدعى (رأس المخروط).

حساب حجم المخروط الدوراني بالتكامل

ما هو حساب حجم المخروط الدوراني بالتكامل، قد ورد أنه يعني أن الجسم الناشئ من دوران شكل ما، وأن هذا الجسم هندسي مستوٍ حول مستقيم، يعد في الحقيقة هو الجسم الدوراني الواقع في مستوى الشكل الهندسي، على سبيل المثال:

• ينشأ من خلال دوران مثلث قائم حول أحد ضلعي القائمة، المخروط الدائري القائم، حيث يكون الضلع محور الدوران.
• بالإضافة إلى أنه سيتم ذكر ما إذا كان محور الدوران محور السينات أو محور الصادات.

من أجل أن يتوفَّر لدينا المنحنىٰ ص = د(س)، والمطلوب هو الحصول على الحجم الناشئ من دوران المساحة التي يكمن بـمنحنى الدالة والمُستقيمان:

• س = أ، س = ب حول محور السينات؛ ولذلك يتم تقسيم المساحة إلى مستطيلات صغيرة.
• بحيث يكون الحجم النهاية لمجموع المستطيلات التي نشأت من خلال دوران هذه المستطيلات وعن طريق اعتبار (ص) طول مستطيل، (∆ س) العرض.
• وبالتالي ـيكون حجم الأسطوانة الذي نحصل عليه = ط ص² × ∆س.

كما يمكنك التعرف على: كيفية حساب مساحة المخروط

قانون حجم المخروط

من أهم الأشياء التي يجب نعلمها لإيجاد قوانين الحجم والمساحة للمخروط:

• نصف القطر: يعد المسافة التي تكون بين مركز القاعدة الدائرية، ومحيطها.
• كما أن الارتفاع: يعد العمود المُقام بين مركز القاعدة الدائرية، والرأس المُدبب للمخروط؛ حيث يتم صنع زاوية قائمة مع القاعدة الدائرية.
• المائل: أو يدعى الارتفاع الجانبي، يعد المسافة بين أية نقطة موجودة على محيط القاعدة الدائرية، والرأس المدبب.

حجم المخروط= 1/3× مساحة القاعدة ×الارتفاع.

رمزيًا: حجم المخروط = 1/3× (π×نق²) × ع؛ نظرًا لأن مساحة القاعدة = π × نق²؛ ويُعد:

• نق: نصف قطر القاعدة.
• ع: ارتفاع المخروط.
• وπ: عدد ثابت، يُقدَّر بـ 3.14 أو 22/7.

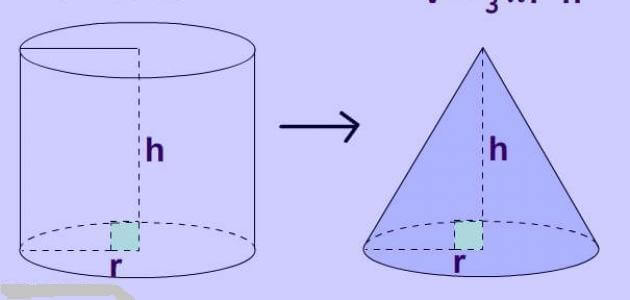
ملاحظة: هناك علاقة بين حجم المخروط والأسطوانة وهي أشبه بالعلاقة بين حجم الهرم والمنشور.

فـحينما يكون ارتفاع المخروط والأسطوانة متساوي، سيكون حجم الأسطوانة مساويًا لـحجم المخروط بـمقدار ثلاثة أضعاف.

قانون حجم المخروط المقطوع والمائل

يعد المخروط الذي تم قطع جزء من أعلاه بحيث يكون القطع بشكل عمودي على الارتفاع، فـهو (المخروط المقطوع).

وعن طريق طرح حجم الجزء الذي تم قطعه من المخروط الكبير الذي لديه القاعدة يمكن حساب (حجم المخروط المقطوع)، أو يمكننا اتباع الصيغة التالية:

• حجم المخروط المقطوع= (1/3× π× ع× (نق*)²+(نق*×نق) + (نق)²)، ويُعد:
• نق: نصف قطر القاعدة السفلية للمخروط الناقص.
• نق: نصف قطر القاعدة العلوية للمخروط المقطوع.
• ع: ارتفاع المخروط المقطوع.

كما نجد أن المخروط الذي لا تسقط قمته على استقامة واحدة مع مركز القاعدة، هو (المخروط المائل).

والذي يتم حساب حجمه من خلال نفس الطريقة التي يحسَب بها حجم المخروط القائم.

أمثلة على حساب حجم المخروط

المثال الأول

مخروط ارتفاعه 18سم، ونصف قطره 8سم، اذكر حجمه.

الحل:

• نصف قطر المخروط يساوي 8.
• كما أن ارتفاع المخروط يساوي 18.

وبالتعويض بالقيم المذكورة في قانون حجم المخروط، وهو: حجم المخروط= 1/3× مساحة القاعدة× الارتفاع، يكون الناتج:

• حجم المخروط= 1/3×3.14×8²×18=1,205.76سم³.

المثال الثاني

مخروط نصف قطره 12سم، وارتفاعه 14سم، اذكر حجمه.

الحل:

• نصف قطر المخروط يساوي 12.
• بالإضافة إلى أن ارتفاعه يساوي 14.

وبالتعويض بالقيم المذكورة في قانون حجم المخروط، وهو: حجم المخروط= 1/3× مساحة القاعدة× الارتفاع، الناتج هو:

حجم المخروط= 1/3×3.14×12²×14=2,111سم³.

المثال الثالث

مخروط مقطوع يبلغ طول نصفي قاعدتيه 6سم، 2سم، وارتفاعه 10سم، فما حجمه؟

الحل:

وعند استخدام القانون: حجم المخروط المقطوع= 1/3×π×ع×((نق*)²+(نق*×نق)+(نق)²)، والتعويض بالقيم المذكزرة فيه، الناتج هو:

• حجم المخروط المقطوع= 1/3×3.14×10×((2)²+(2×6)+(6)²)=544.54سم³.

المثال الرابع

مخروط قطره 15سم، وارتفاعه 16سم، اذكر حجمه.

الحل:

• ونجد أن قطر المخروط يساوي 15سم، إذًا فإن نصف قطره هو: 15/2=7.5سم، وارتفاعه يساوي 16،

وعند التعويض بالقيم المذكورة في قانون حجم المخروط، وهو: حجم المخروط= 1/3×مساحة القاعدة×الارتفاع، الناتج هو:

حجم المخروط= 1/3×3.14×7.5²×16= 942سم³.

المثال الخامس

مخروط نصف قطره 24سم، وارتفاعه الجانبي 25سم، اذكر حجمه.

الحل:

• كما أن حساب ارتفاع المخروط من ارتفاعه الجانبي، وذلك من خلال استخدام القانون الآتي: الارتفاع الجانبي= (مربع الارتفاع+مربع نصف القطر)√؛ حيث: الارتفاع=(25²-² 24)√= 7سم.

وبالتعويض بالقيم المذكورة في قانون حجم المخروط، وهو: حجم المخروط= 1/3×مساحة القاعدة×الارتفاع، الناتج هو:

ونجد حجم المخروط= 1/3×3.14×24²×7= 4,220.16سم³.

المثال السادس

في حالة كان معدل سقوط الرمل من المخروط العلوي إلى المخروط السفلي في ساعة رملية تتكون من مخروطين يتقابل رأسيهما في نفس النقطة هو 50مم³/ثانية.

كما أن ارتفاع الرمل في المخروط العلوي يبلغ 24مم، ونصف قطره فهو 10مم، حدد المدة اللازمة لانتقال الرمل كاملًا من المخروط العلوي نحو السفلي.

الحل

وعند التعويض بالقيم المذكورة في قانون حجم المخروط لحساب حجم الرمل في المخروط العلوي، وهو: حجم المخروط= 1/3×مساحة القاعدة × الارتفاع، الناتج هو: حجم الرمل في المخروط العلوي= 1/3×3.14×10²×24= 2,512مم³.

كما أن حساب المدة الزمينة اللازمة كي ينتقل الرمل من المخروط العلوي إلى السفلي، من خلال قسمة حجم الرمل على معدل سقوطه؛ والناتج هو: المدة الزمينة اللازمة لانتقال الرمل بالكامل= 2,512/50=50.24 ثانية.

شاهد أيضًا: كيفية حساب مساحة المخروط

المثال السابع

مخروط مائل قطره 12م، وارتفاعه 15م، اذكر حجمه.

الحل:

• قطر المخروط يساوي 12م، إذًا فإن نصف قطره هو: 12/2=6م.
• وارتفاعه يساوي 15م.

وبالتعويض بالقيم المذكورة في قانون حجم المخروط، وهو: حجم المخروط= 1/3×مساحة القاعدة×الارتفاع، الناتج هو:

حجم المخروط= 1/3×3.14×6²×15= 565.2م³.

المثال الثامن

إذا كان حجم المخروط هو 169سم³، ونصف قطره 4سم، فما هو ارتفاعه؟

الحل:

بالتعويض بالقيم المذكورة في قانون حجم المخروط، وهو:

• حجم المخروط= 1/3×مساحة القاعدة×الارتفاع.
• الناتج هو: 169= 1/3×3.14×4²×الارتفاع، ومنه الارتفاع= 10.1سم.

المثال التاسع

محيط قاعدة خيمة على شكل مخروط هو 44م، احسب كمية الهواء الموجودة داخلها، مع العلم أن ارتفاعها هو 9م.

الحل:

• كمية الهواء الموجودة داخل الخيمة تساوي حجم الخيمة مخروطية الشكل.
• إذًا يجب حساب حجم الخيمة بالتعويض بالقيم المذكورة في قانون حجم المخروط.

إلا أنه يجب أولًا إيجاد نصف قطر القاعدة الدائرية عن طريق استخدام قانون محيط الدائرة، وهو:

محيط الدائرة=2×π×نق، ومنه: 44=2×3.14×نق، وعليه: نق=7م، وهو نصف قطر الخيمة.

بالإضافة إلى التعويض بالقيم المذكورة في قانون حجم المخروط= 1/3×مساحة القاعدة×الارتفاع، الناتج هو:

حجم الخيمة=1/3×3.14ײ7×9=462م³، وهو كمية الهواء الموجودة بداخلها.

المثال العاشر

حجم المخروط يساوي 9π وحدة مكعبة، ويبلغ ارتفاعه قيمة مساوية لـنصف قطره، احسب قيمة نصف قطره.

الحل:

مع افتراض أن قيمة نصف القطر = س، وهي تساوي الارتفاع، وفقًا لـمعطيات السؤال، وبالتعويض بالقيم المذكورة في قانون حجم المخروط، الناتج هو:

حجم المخروط=1/3 × مساحة القاعدة × الارتفاع، ومنه: 1/3×π×س²×س=9π.

وبتبسيط المعادلة، ثم أخذ الجذر التكعيبي للطرفين، الناتج هو:

س=3 وحدات، وهي قيمة كل من الارتفاع، ونصف القطر.

المثال الحادي عشر

ارتفاع مخروط كبير الحجم 18م، ونصف قطره 4م، ويمكن ملؤه بالماء بمعدل يبلغ 3م³ كل 25 ثانية، قم بحساب المدة اللازمة كي يمتلئ المخروط بالكامل.

الحل:

لإيجاد سعة المخروط من الماء حساب حجمه، باستخدام القانون: حجم المخروط=1/3×مساحة القاعدة×الارتفاع، ومنه: حجم المخروط=1/3×3.14×4²×18=301.44م³.

كما أن حساب المدة اللازمة كي يمتلئ المخروط= حجم المخروط/معدل امتلائه بالماء=301.44م³÷(3م³/ 25ثانية)=2512 ثانية=41 دقيقة و53 ثانية.

هنا تجد أيضًا: نشأة الهندسة التحليلية وعلاقتها بفروع الرياضيات المختلفة

حساب حجم المخروط الدوراني بالتكامل، مفهوم حجم المخروط (Cone Volume) أنه مقدار الحيِّز الذي يشغَل من الجسم ثلاثي الأبعاد، أو هو مقدار سعته، ويتم القياس بالكثير من الوحدات المُكعبة، مثل إنش³، قدم³، سم³، م³.