محيط الدائرة وقوانينها
محيط الدائرة وقوانينها، كثيراً ما يلجأ إلينا أبنائنا من أجل مساعدتهم في الإجابة على بعض المسائل الرياضية التي يصعب عليهم حلها، ولكن للأسف لا نستطيع أن نجيبهم على تساؤلاتهم لعدم معرفتنا ببعض القوانين والمعادلات المستخدمة في حل تلك المسائل الحسابية، ولذلك أعددنا لكم هذا المقال حتى تجدون الإجابة النموذجية لجميع الأسئلة.
محتويات المقال
مفهوم الدائرة
هناك عدة مفاهيم تم تداولها علماء الرياضيات بخصوص تعريف الدائرة، وسوف نوضح فيما يلي أشهر تلك التعريفات:
- يمكن تعريف الدائرة بأسلوب بسيط على أنها شكل من الأشكال الهندسية ثنائي الأبعاد، ويتم رسمها على شكل قوس أو منحنى، وهي تبعد بمقدار مسافة ثابتة عن نقطة تقع في منتصفها، ويتم تسمية تلك المسافة التي تفصل بين نقطة المركز وذلك المنحنى باسم نصف قطر الدائرة.
- كما يمكن تعريفها أيضاً بأنها شكل من الأشكال بحيث تبعد جميع نقاطه بنفس قيمة المقدار أي بمقدار ثابت عن مركزه، كما يتم تسمية الدائرة باسم مركزها، فعلى سبيل المثال إذا كان يطلق على مركز الدائرة اسم (س) فإن تلك الدائرة سوف تسمى (س).
- كما أوضح آخرون أن الدائرة هي عبارة عن عدة نقاط تم رسمها على سطح معين، وجميع تلك النقاط تبعد بمسافات متساوية عن نقطة تقع في منتصف تلك النقاط تسمى المركز، في حين تسمى المسافة بين أي نقطة من هذه النقاط ومركز الدائرة باسم نصف قطر الدائرة.
- وأخيراً تم تعريف الدائرة بأنها ذلك المنحنى المغلق الذي تم توصيل جميل نقاطه ببعضها، وجميع تلك النقاط تبعد بعد ثابت عن نقطة ثابتة تقع في منتصف الدائرة تسمى مركز الدائرة، ويرمز للمسافة بين ذلك المنحنى ومركز الدائرة بالرمز (نق).
شاهد أيضًا: كيفية حساب الوزن المثالي بالنسبة للطول والعمر
محتويات الدائرة
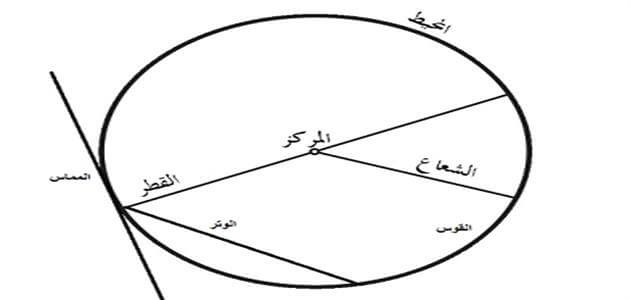
تحتوي الدائرة على عدة أجزاء مختلفة، وكل جزء له تعريف خاص به، ويمكن توضيح تلك الأجزاء فيما يلي:
1ـ مركز الدائرة
مركز الدائرة يعتبر النقطة المرجعية للدائرة، وتبعد عنها جميع النقاط الواقعة على محيط الدائرة بمسافة ثابتة.
2ـ القوس
هو عبارة عن أي جزء من محيط الدائرة.
3ـ نصف قطر الدائرة
يرمز لنصف قطر الدائرة بالرمز (نق)، وهو ذلك الخط المستقيم الواصل ما بين نقطة مركز الدائرة وأي نقطة أخرى على هذه الدائرة.
4ـ قطر الدائرة
يرمز لقطر الدائرة بالرمز (ق)، وهو ذلك الخط المستقيم الذي يصل ما بين نقطتين في الدائرة ويمر في نقطة مركز الدائرة.
5ـ القطاع
هي تلك المنطقة التي تقع ما بين نصفي قطرين مختلفين في الدائرة.
6ـ وتر الدائرة
هو ذلك الخط المستقيم الذي يصل ما بين أي نقطتين على محيط الدائرة، ولكنه لا يمر بنقطة مركز الدائرة.
7ـ القطعة
هي تلك المنطقة التي تقع ما بين أي وتر في الدائرة ومحيطها.
8ـ المماس
هو ذلك الخط المستقيم المرسوم خارج الدائرة، حيث يلامس هذا المستقيم الدائرة عند نقطة وحيدة.
مواصفات أقطار الدائرة
أقطار الدائرة لها العديد من المواصفات والتي يمكن إيضاحها فيما يلي:
- أقطار الدائرة الواحدة دائماً تكون متساوية.
- أقطار الدائرة الواحدة تمثل محاور متماثلة.
- يعتبر مركز الدائرة هو تلك النقطة التي تلتقي فيها جميع أقطار الدائرة.
أجزاء الدائرة
تقسم الدائرة إلى جزئيين أساسيين وهما:
1ـ جزء داخلي
يطلق على الجزء الداخلي للدائرة اسم مساحة الدائرة، ويتم قياس مساحة الدائرة بوحدة المتر المربع (م2).
2ـ جزء خارجي
يطلق على الجزء الخارجي للدائرة اسم محيط الدائرة، ويتم قياس مساحة الدائرة بوحدة المتر (م).
شاهد أيضًا: كيف اعرف مقاس الخاتم؟
محيط الدائرة وقوانينها
مفهوم محيط الدائرة
يمكننا تعريف محيط أي شكل من خلال معرفة طول الحواف المحيطة بهذا الشكل من الجهة الخارجية، ومن هنا يمكننا التوصل إلى مفهوم محيط الدائرة بأنها هي تلك المسافة التي تم قياسها حول الدائرة.
قوانين الدائرة
ويمكن حساب محيط الدائرة من خلال ضرب قطر الدائرة في ذلك العدد الذي يسمى باي ويطلق عليه في اللغة الإنجليزية اسم Pi ويرمز له بالرمز π.
ويمكن توضيح قوانين الدائرة من خلال المعادلات التالية:
- محيط الدائرة = قطر الدائرة * π.
- مساحة الدائرة = (قطر الدائرة/2)2 * π.
مفهوم الرمز باي π
قام علماء الرياضيات بالرمز للعدد باي بالرمز الإغريقي π والذي يساوي قيمته حسابياً 3.14159265358979323846، ويتم تقريب ذلك العدد إلى 3.14.
ويرجع حساب هذا العدد من خلال حساب المسافة حول الدائرة والتي يطلق عليها محيط الدائرة ثم تقسيمها على الخط المستقيم الواصل ما بين منحنيين في الدائرة والذي يمر في نقطة مركز الدائرة ويطلق عليه قطر الدائرة ومن ثم ينتج العدد باي، ويمكن توضيح ذلك من خلال المعادلة التالية:
π = محيط الدائرة / قطر الدائرة.
أمثلة متنوعة على حساب محيط الدائرة
مثال رقم (1)
دائرة قطرها 4 سم احسب محيط تلك الدائرة
الحل:
بالرجوع إلى قانون حساب محيط الدائرة يمكننا الوصول إلى الناتج من خلال ما يلي:
محيط الدائرة = قطر الدائرة * π.
محيط الدائرة = 4 * 3.14.
محيط الدائرة = 12.56 سم.
مثال رقم (2)
دائرة نصف قطرها 3 سم احسب محيط تلك الدائرة
الحل:
بالرجوع إلى قانون حساب محيط الدائرة يمكننا الوصول إلى الناتج من خلال ما يلي:
محيط الدائرة = قطر الدائرة * π.
محيط الدائرة = 2* نصف قطر الدائرة * π.
محيط الدائرة = 2 * 3 * 3.14.
محيط الدائرة = 18.84.
مثال رقم (3)
دائرة محيطها 12.56 سم احسب قطر هذه الدائرة
الحل
بالرجوع إلى قانون حساب محيط الدائرة يمكننا الوصول إلى الحل من خلال ما يلي:
محيط الدائرة = قطر الدائرة * π.
12.56 = قطر الدائرة * 3.14.
قطر الدائرة = 12.56 / 3.14.
قطر الدائرة = 4 سم.
مثال رقم (4)
مشتل أزهار على شكل دائري، يبلغ نصف قطره 9 أمتار، احسب محيطه
الحل
بالرجوع إلى قانون حساب محيط الدائرة يمكننا الوصول إلى الناتج من خلال ما يلي:
محيط الدائرة = قطر الدائرة * π.
محيط الدائرة = 2 * 9 * 3.14.
محيط الدائرة = 56.52.
طريقة رسم الدائرة
يستخدم الفرجار الذي يطلق عليه باللغة الإنجليزية اسم Compass من أجل رسم دائرة محكمة على أي سطح أملس، والفرجار هو عبارة عن أداة هندسية تتكون من ذراعين تم تعليقهم معاً بطريقة تسهل تحريكهم، ويكون إحدى هذين الذراعين ذو رأس مدبب، أما الذراع الآخر فيتم تثبيت فيه قلم رصاص.
ويمكن استخدام الفرجار لرسم دائرة كاملة أو لرسم أجزاء من الدائرة.
خطوات رسم الدائرة
يمكنك رسم دائرة بطريقة سهلة من خلال إتباع الخطوات التالية:
- تأكد من أن رأس الفرجار ثابتة حتى تضمن ثبات الفرجار وعدم انزلاقه أثناء القيام بعملية الرسم.
- تأكد من أن القلم الرصاص ثابت حتى لا يسقط القلم من الفرجار أثناء عملية الرسم.
- اجعل رأس القلم في نفس مستوى الذراع الأخرى للفرجار.
- قم بتثبيت الرأس المدبب للفرجار على السطح الذي تريد الرسم عليه، ثم قم بتحريك الفرجار بشكل دائري حول رأسه حتى تتمكن من رسم جزء من الدائرة أو لرسم دائرة كاملة.
- إذا أردت أن ترسم دائرة بنصف قطر معين فيمكنك استخدام المسطرة لتحديد فتحة الفرجار حتى ترسم دائرة بنفس طول نصف القطر المراد رسمه.
شاهد أيضًا: 7 خطوات لعمل مجسم هرمي هندسي بالكرتون والورق
وبذلك نكون قد انتهينا اليوم من مقالنا عن محيط الدائرة وقوانينها، نتمنى أن نكون قدمنا لكم إجابة على جميع تساؤلاتكم، فنحن نحرص على توضيح كافة المعلومات مهما كانت تبدو بسيطة مع توضيح أمثلة مختلفة من أجل ضمان ثبات المعلومة، وننتظر تعليقاتكم وأسئلتكم دائماً.