الزوايا المتتامة والزوايا المتكاملة
الزوايا المتتامة والزوايا المتكاملة، موقع مقال mqaall-com يقدم لكم الزوايا المتتامة والزوايا المتكاملة، حيث تعد هاتان الزاويتان من أشهر أنواع الزوايا، ولكل منهما خصائص وقواعد مختلفة، وسنتعرف معًا بهذا المقال على خصائصهم بكل سلاسة.
محتويات المقال
مفهوم الزَاوية
قبل على الزوايا المتتامة والزوايا المتكاملة يمكننا أن نعرِّف الزاوية (Angle) كـ مقدار الانفراج الذي يحصره خطان مستقيمان أي كلٍ منهما ضلع للزاوية.
وحين تلاقيهما مع بعضهما البعض يشكلان نقطة تدعى رأس الزاوية (Vertex).
وهناك مفهوم آخر سـنطرحه معًا: الزاوية عبارة عن شعاعين كل منهما ينطلق من نقطة بداية واحدة.
كما يمكنك التعرف على: خواص متوازي الاضلاع من حيث الزوايا
وهناك سؤال هام سـيخطر بأذهاننا، كيف نعبِّر عن الزاوية؟
- هناك طريقة لـتسميتها بثلاثة حروف لكل رأس حرف ورأس الزاوية المطلوبة يكون الحروف الأوسط، على سبيل المثال: الزاوية (أ ب ج).
- أو من خلال تسمية رأس الزاوية فقط، في حالة لم يشاركها به آخر.
- ويمكننا أن ندعيها بـحرف إغريقي معبِّرًا عن قياسها، مثل: (α),(θ).
- وحدة قياس الزاوية الدرجات كما يعلم الأغلب منا، ونرمز للدرجة بالرمز (°).
الزوايا المتتامة والزوايا المتكاملة
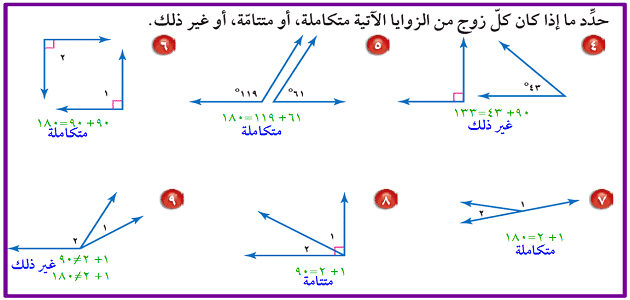
- الزوايا المتتامة: تعد الزوايا المُتتامة مساوية لـ ٩٠ درجة حينما يتم جمع قياسها.
- أما الزوايا المتكاملة: تُعد الزوايا المُتكاملة مساوية لـ ١٨٠ درجة حينما يتم جمع قياسها.
أنواع الزوايا وفقًا لـقياسها
هناك أنواع رئيسية عديدة يتم تصنيف الزاوية من خلالها وفقًا لـقياسها:
- الزَّوايا القائمة (Right Angle): هي زوايا يعد قياسها مساويًا لـ ٩٠ درجة.
- والزَّوايا الحادة (Acute Angle): هي زوايا يكون قياسها أكبر من الصفر وأصغر من قياس الزاوية القائمة، أي قياسها متراوح بين 0° إلى 90°.
- الزَّوايا المُنفرِجة (Obtuse Angle): هي زوايا يكون قياسها كبير عن 90° وصغير عن 180°.
- بالإضافة إلى الزّوايا المستقيمة (Straight Angle): هي زوايا يعد قياسها مساويًا لـ 180°، أي تظهر بهيئة خط مستقيم.
- الزَّوايا المُنعكِسة (Reflex Angle): هي زوايا يكون قياسها يكبر عن 180° ويصغر عن 360°.
- والزّوايا الكاملة (Full Angle): هي زوايا يعد قياسها مساويًا لـ 360°، مما يعني أنها زوايا تقوم بعمل دورة كاملة؛ حيث تنتهي عند النقطة التي بدأت منها منذ المرة الأولى.
أنواع الزوايا وفقًا لاتجاه قياسها
وهناك أنواع عديدة وتصنيف آخر للزوايا من حيث اتجاه الدوران أو قياسها:
- الزوايا الموجبة (Positive Angles): هي زوايا يمكننا قياسها من خلال اتجاه عكس اتجاه دوران عقارب الساعة حينما يتم البدء من القاعدة.
- والزوايا السالبة (Negative Angles): هي زوايا يمكننا قياسها بالاتجاه الموافق لاتجاه دوران عقارب الساعة حينما نبدأ من القاعدة.
أنواع زوايا وفقا لعلاقات تربطها معا
لنتعرف على الزوايا المتتامة والزوايا المتكاملة فهناك زوايا يتم إطلاق أسماء خاصة لها وفقًا لعلاقات معنية تربطها، ومنها ما سنذكره أدناه:
- الزوايا المتجاورة (Adjacent Angles): هي زوايا متشاركة مع بعضها البعض في ضلع واحد ورأس واحدة أيضًا.
- والزوايا المتتامة (Complementary Angles): هي زوايا تجاور بعضها ويكون حاصل جمع قياسها مساويًا لـ 90°.
- الزوايا المتكاملة (Supplementary Angles): هي زوايا تجاور بعضها ويكون حاصل جمع قياسها 180°؛ مما يعنى أنها زوايا تقوم بتشكيل “زاوية مُستقيمة”.
- بالإضافة إلى الزوايا المتقابلة بالرأس (Vertically Opposite Angles): هي زوايا تكون ناتج لـتقاطع خطين مستقيمين التقيا في نقطة واحدة، وهذه النقطة تدعىٰ (رأس الزاويتين المتقابلتين)، ومن خواص هذه الزاويا تساويها في القياس وأضلاعها تكون على امتداد واحد.
- والزوايا المتطابقة (Congruent angles): هي زوايا قياس كل منها مساوٍ للأخرى.
اقرأ من هنا عن: بحث عن تأثير اختلاف الزوايا في دقة القياسات
أنواع الزوايا المتتامة
1_ الزوايا المتجاورة المتتامة
مثلما ذكرنا أعلاه أن الزاويتين المتتامتين مجموع قياسمها ٩٠ درجة، وفي حالة كانت الزوايتان متجاورتان متتامتان.
مما يعني أنهما يتقاطعان في نقطة وضلع ولا يحدث التقاطع في أي نقطة داخلية؛ وبذلك يكون ضلعيهما غير المشتركان صانعي زاوية قائمة.
2-الزوايا المتجاورة المتكاملة
مثلما ذكرنا أعلاه أن الزاويتين المتكاملتين مجموع قياسمها ١٨٠ درجة أي مجموع نصف دائرة؛ حيث يكون مجموعها كاملًا ٢٦٠ درجة، وفي حالة كانت الزوايتان متجاورتان متكاملتان.
مما يعني أنهما يتقاطعان في نقطة وضلع ولا يحدث التقاطع في أي نقطة داخلية؛ وبذلك يكون ضلعيهما غير المشتركان صانعي خط مستقيم.
قاعدة الزوايا المتكاملة
- التعبير اللفظي المعروف للزوايا المُتكاملة هو: أن الزاويتين المتكاملتين يكون حاصل جمع قياسهما مساويًا لـ 180°.
- في حالة تجاور الزاويتين أي تشاركهما في ضلع مستقيم من أحد الأضلاع، متصل به ضلع آخر.
- بالتالي سيكون الناتج لدينا هي زاوية بجهة اليمين وأخرى بجهة اليسار.
- إذًا في هذه الحالة ستكون الزاويتان متكاملتين.
- دومًا ما نرى الترابط بين الزوايا المتكاملة والزوايا المُتتامة.
- التي يكون حاصل جمع قياسها 90°.
على سبيل المثال
- هناك قطعة مستقيمة يوجد عليها ضلع يقسمها إلى زاويتين، فـنتجت زاوية منفرجة = 120°.
- وزاوية أخرى حادة = 60°؛ بما أن مجموعها مساويًا لـ 180° أي هما زاويتان متكاملتان.
- ولكن إذا وجِد أن قياس أحد الزوايا = 40°، والزاوية الأخرى = 50°.
- فـبما أن مجموعها مساويًا لـ 90° أي هما زاويتان متتامتان.
- في حالة تواجد الضلع المشترك على الخط المستقيم بشكل عمودي أي زاويته قائمة.
- فـمن الطبيعي ستكون الزاويتان متكاملتين من كلا الجانبين.
- كما سنرى أن كل زاوية قائمة أي = 90°؛ فبالتالي 90+90=180°.
حالات الزوايا المتكاملة
هذه هي الحالات التي حينما نستخرج ناتج حاصل جمع قياس زواياها سـتعطينا 180°، ومنها:
- نظرًا لأن الزاوية القائمة هي الزاوية التي تساوي 90° فـحين وجود زاوية قائمة مع أخرى قائمة 90+90=180°.
- ونظرًا لأن الزاوية الحادة هي التي تتراوح ما بين 0° إلى 90°، والزاوية المُنفرجة هي التي أكبر من 90° وأقل من 180°:
- فـحين وجود زاوية حادة مع أخرى مُنفرجة 40+140=180° والعكس، فـحين وجود زاوية منفرجة مع زاوية حادة 91+89= 180°.
- ومن ضمن المسائل التي تأتي للطلاب، أن يكون المُعطى قياس إحدى الزوايا، والمطلوب منك إيجاد الزاوية الأخرى؛ وذلك مع العلم أن الزاويتين متكاملتين أي حاصل جمع قياسهما =180°.
على سبيل المثال
قم بإيجاد الزاوية المطلوبة، مع العلم أن الزاوية (ب) المجاورة لها تساوي 50°.
الحل
نظرًا لـتجاور الزاويتين، فـهما زاويتان متكاملتان مما يعني أن حاصل جمع قياسهما = 180°
وبذلك يكون قياس الزاوية (ب) =180-50= 130°.
مثال آخر
هناك ضلع (س) متعامد على الضلع الآخر (ص)، مما أدى لصنع الزاويتين (أ) و(ب)، قم بإيجاد حاصل جمع قياس الزاويتين.
الحل
بما أن الزاويتين متكاملتين أي حاصل جمع قياسهما مساويًا لـ 180°؛ نظرًا لأن الضلع يتعامد على الآخر فـالناتج يكون زاويتان قائمتان، مما يعني أن كل زاوية قائمة = 90°، إذًا حاصل جمع قياسهما = 180°.
خطوات رسم زاوية
يوجد بعض الخطوات التي لا بد من اتباعها من أجل رسم زاوية لها قياس معين، عن طريق استعمال (المنقلة والمسطرة)؛ فـمثلًا عند رسم زاوية ذات قياس 30°، سـنتمكن من ذلك عند اتباع الخطوات التالية:
- يتم الرسم بالمسطرة قطعة مستقيمة، وتدعى القطعة (س ص).
- كما يتم وضع المنقلة على القطعة المُستقيمة التي تم رسمها (س ص).
- بـحيث يتم انطباق مركزه المنقلة على نقطة رأس الزاوية التي تمثلها النقطة (ص).
- إلى جانب وضع تدريج هذه المنقلة البادئ من درجة 0° على الضلع (س ص)، ومن ثَم يتم تعيين مكان الزاوية 40° بدقة عالية على المنقلة.
- يتم تعيين الـ 40° عن طريق وضع نقطة أو أي علامة بالقلم، وتدعى هذه النقطة (ع).
- بالإضافة إلى أنه يتم رسم خط مستقيم يكون الاتصال بين نقطة (ع) و(ص).
- كما سيتم الحصول على زاوية حادة قياسها 40° (س ص ع)، بعد اتباع ما ذكرنا من خطوات.
اقرأ أيضاً: بحث عن الزوايا والمستقيمات المتوازية في الرياضيات
الزوايا المتتامة والزوايا المتكاملة، استعرضنا معًا بهذا المقال ما يمكننا الاستفادة منه بهذه الزوايا وأمثلة سـتعمل على التيسير من فهمها.