تعريف شبه المنحرف في الرياضيات
تعريف شبه المنحرف في الرياضيات من الأمور التي تهم للمهتمين بعلم الرياضيات حيث يعتبر من عائلة الأشكال الهندسية الرباعية، والتي يجب أن نعرف خصائصه والأنواع المختلفة لشبة المنحرف، وهذا ما سنتعرف عليه من خلال مقالنا بالتفصيل.
محتويات المقال
تعريف شبه المنحرف في الرياضيات
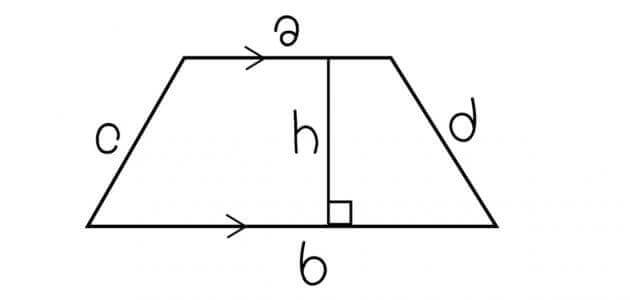
- تم تعريف شبه المنحرف في الرياضيات أنه هو شكل من الأشكال الهندسية التي تتكون من أربعة أضلاع، ويكون به ضلعان متقابلان متوازيان، ويعرف كل ضلع منهما بأنه قاعدة لشبه المنحرف.
- وعند تعريف شبة المنحرف بشكل آخر، نجد أنه الشكل المسطح الذي توجد به أربعة أضلاع مستقيمة، وتعرف الأضلاع الغير متوازية بأنها ساق شبه المنحرف، والأضلاع المتقابلة تمثل قاعدته.
- ويكون الضلع الأطول في شبة المنحرف هو القاعدة السفلية له، أما الأضلاع المائلة هي القاعدة العليا له، وفي الغالب تكون القواعد العليا أقصر طولا من القواعد السفلية.
- في تعريف شبه المنحرف في الرياضيات، نجد أنه يطلق عليه اسم مثلث مقطوع الرأس، ويعتبر أيضا من الأشكال ذات الأبعاد الثلاثية.
اقرأ من هنا عن: موضوع تعبير عن مساحة شبه المنحرف
ما هي خصائص شبه المنحرف؟
- يضم شبة المنحرف أربعة زوايا، ويكون مجموع قياس تلك الزوايا يساوي 360 درجة.
- في شبه المنحرف تكون كل زاويتين متجاورتين متكاملتين، ويكون مجموع قياسهما 180 درجة، أي الزوايا الموجودة في الأسفل، والزوايا العلوية
- تتوازي قاعدتي شبة المنحرف، وتسمى الرؤوس الأربعة الموجودة به بزوايا شبة المنحرف.
- الأضلاع الأربعة في شبه المنحرف غير متساويين، فاثنان منهم متوازيين، والآخرين غير متوازيين.
- يتقاطع قطري شبة المنحرف في نقطة التقاء واحدة، وتقع تلك النقطة على خط مستقيم مع نقطة التقاء الأضلاع المقابلة.
- يتم حساب قيمة الخط الواصل بين منتصف الأضلاع الغير متوازية من خلال حساب الوسيط للقاعدة العليا والسفلي لشبه المنحرف، ويكون القانون كالتالي.
- طول الخط المتوسط = طول القاعدتان المتوازيتان / 2.
خصائص شبه المنحرف متساوي الساقين
يتميز شبه المنحرف متساوي الساقين بمجموعة من الخصائص ومنها:
- الأقطار الموجودة داخل شبه المنحرف متساوي الساقين تكون متطابقة، أي تتساوى في الطول.
- الأضلاع الغير متوازية تكون متساوية في الطول أيضا.
- الزوايا الخاصة بالقاعدة السفلية بشبه المنحرف تتطابق من حيث القياس، وذلك أيضا في زوايا القاعدة العليا.
- تعتبر زوايا القاعدة العليا في شبه المنحرف زوايا متكاملة مع زوايا القاعدة السفلية، وذلك يعني أنهم يصنعوا زاوية ذات قياس 180 درجة.
أنواع شبة المنحرف
1- شبة المنحرف مختلف الأضلاع
- واسمه في اللغة الإنجليزية Scalene trapezoid، وتكون الأضلاع في شبه المنحرف مختلف الأضلاع غير متساوية، وقاعدتيه تكونان متوازيتان، ولكنهما يختلفان من حيث الطول.
- أما الساقيين في شبة المنحرف مختلف الأضلاع فهم غير متوازيان، وغير متساويان في الطول.
2- شبه المنحرف متساوي الساقين
- يكون الساقيين في هذا الشكل متساويان في الطول، ولكن غير متوازيان.
- وتكون القاعدتان العليا والسفلى أيضا متوازيتان، ولكنهم غير متساويان من حيث القياس.
3- شبة المنحرف ذات الزوايا الحادة ((Acute trapezoid
تكون الزوايا الموجودة بين القاعدة الأطول وبين الساقين قياسها أقل من 90 درجة، والتي تعرف بالزاوية الحادة.
4- شبة المنحرف منفرج الزاوية (Obtuse trapezoid)
- شبة المنحرف منفرج الزاوية هو ذلك الشكل الذي تكون الزاوية الموجودة بين القاعدة وأحد الساقين منفرجة.
- وتعرف الزاوية المنفرجة بأنها الزاوية التي يكون قياسها أكثر من 90 درجة وأقل من 180 درجة.
5- شبه المنحرف قائم الزاوية (Right trapezoid)
تكون الزوايا الواقعة بين القاعدة العليا والسفلي، وإحدى الساقين، تكون قائمة، وقياسها 90 درجة.
أمثلة على خصائص شبه المنحرف
- شبه المنحرف (أ ب ج د)، وطول قاعدته العليا (أ ب) هو 12 سم، وطول قاعدته السفلى (ج د) هو 18 سم، وطول الخط الواصل بين منتصفي الضلعين الغير متوازيين هو 2 ص – 1، فما قيمة ص.
- الحل: الخط المتوسط = مجموع طول القاعدتين/2= (12 +18)2 = 2/30= 15 سم.
ولا يفوتك قراءة مقالنا عن: مساحة شبه المنحرف متساوي الساقين والقائم
كيف يتم حساب ارتفاع شبه المنحرف؟
- هناك قانون يتم من خلاله حساب ارتفاع شبه المنحرف، والقانون هو:
ارتفاع شبة المنحرف = طول الضلع المقابل للارتفاع × جا الزاوية السفلية الواقعة بين هذا الضلع والقاعدة السفلية.
- وللتوضيح أكثر يمكن تسمية أضلاع شبة المنحرف بالرموز التالية (أ ب ج د)، ويمثل القاعدة السفلية لشبة المنحرف (أ ب)، والقاعدة العلوية تمثل (د ج).
- فيكون قانون حساب ارتفاع شبه المنحرف بالرموز هو:
- الارتفاع= طول الضلع (أ د) × جا الزاوية (أ).
- الارتفاع = طول الضلع (ب ج) × جا الزاوية (ب).
حساب أقطار شبه المنحرف
لحساب طول القطر في شبة المنحرف (أ ب ج د) وتكون القاعدة السفلية له (أ ب)، والقاعدة العليا هي (ج د)، ويكون القانون هو:
- طول القطر الأول (أ ج) = الجذر التربيعي للقيمة ((أب)2+ (ب ج)2 _ 2× (أب) (ب ج) × جتا (الزاوية المحصورة بينهم)).
- طول القطر الثاني (ب د) = الجذر التربيعي للقيمة ((أ د)2_2× (أد) (أ ب) × جتا ( الزاوية المحصورة بينهم)).
لحساب طول القطر في شبة المنحرف قائم الزاوية
يتم اتباع نظرية فيثاغورث في حساب طول الأقطار الموجودة في شبة المنحرف قائم الزاوية، والقانون يكون كما يلي:
- طول القطر الأول= الجذر التربيعي لمجموع مربعي طول الساق القائم على القاعدتين، وطول القاعدة السفلى.
- طول القطر الثاني= الجذر التربيعي لمجموع طول الساق القائم على القاعدتين، وطول القاعدة العلوية.
- ويمكن استنتاج القانون من خلال استخدام رموز لشبة المنحرف مثل (س ص د ع)، وتكون الزاوية القائمة عند (س) و(ص)، ويصبح قانون نظرية فيثاغورث في حساب أطوال أقطار شبه المنحرف:
- طول القطر الأول= الجذر التربيعي للقيمة (س ص)2+ (ص د)2.
- ويكون طول القطر الثاني= الجذر التربيعي للقيمة (س ص)2+ (س د)
مساحة شبه المنحرف
القانون المستخدم في قياس مساحة شبه المنحرف هو: مساحة شبه المنحرف =1\2 × مجموع طول القاعدتين العلوية والسفلية × الارتفاع.
قانون حساب محيط شبه المنحرف
- محيط شبه المنحرف= مجموع أطوال الأضلاع الأربعة.
- وإذا كان هناك طول أحد الأضلاع غير معروف، يمكن استخدام نظرية فيثاغورس للتوصل لطول هذا الضلع.
أمثلة على حساب محيط شبه المنحرف
المثال الأول
- أوجد محيط شبه منحرف طول أضلاعه الأربعة هم، 6سم، و7 سم، و8 سم، و9 سم.
- يكون الحل باستخدام القانون السابق، وهو مجموع أطوال أضلاعه، ويصبح الناتج 30 سم.
المثال الثاني
- أوجد محيط شبه منحرف متساوي الساقين، إذا كان طول القاعدة السفلية هو 4 أضعاف طول القاعدة العلوية، علما بأن طول القاعدة العلوية يساوي 35 سم، وطول أحد الساقين هو 12.43 سم.
- الحل: طول القاعدة السفلية= 4× طول القاعدة العلوية، وتساوي 4× 7.35= 4 سم، أما محيط شبة المنحرف سيكون= 7.35+29.4 + 12.43+ 12.43، ومجموعهما يساوي 61.61.
- إذا فمحيط شبه المنحرف هو 61 سم.
كما يمكنك التعرف على: مساحة المعين وشبه المنحرف
في ختام مقالنا نكون قد ذكرنا تعريف شبة المنحرف في الرياضيات، وما هي خصائصه، وكيف يمكن حساب محيط شبه المنحرف، والمساحة، وأطوال أقطاره.