طريقة شرح العامل المشترك الأكبر

طريقة شرح العامل المشترك الأكبر، موقع مقال maqall.net يقدم لكم طريقة شرح العامل المشترك الأكبر، حيث طريقة شرح العامل المشترك الأكبر، يتم تعريف العامل المشترك الأكبر على أنه أكبر عامل أو قاسم في العوامل أو القواسم التي تشترك في عددين أو أكثر من ذلك.

طريقة شرح العامل المشترك الأكبر

تابع طريقة شرح العامل المشترك الأكبر فمن أجل استنتاج العامل المشترك الأكبر، سـنتبع الآتي:

• سـنحصل على كافة العوامل الخاصة بـكل عدد، والمقصود بـالعوامل أي الأعداد التي يمكننا ضربها ببعضها من أجل أن يكون الناتج هذا العدد.
• على سبيل المثال: العدد  يكون هذا العدد الناتج حينما نضرب عاملين ببعضهما ألا وهما: 1,8 و2,4.
• إذًا سيتم اتخاذ كل عدد ممَّا ذكرناهم كـعامل من عوامل العدد 8.
• وبعد استنتاج العوامل المشتركة بين العددين، سـنضع حولها دائرة.
• وبالنهاية سـنختار العامل الأكبر بين هذه العوامل المُشتركة التي استخرجناها.

ما هو العامل المُشترك؟

• أكبر عدد يتم من خلاله قسمة العددين معًا بالوقت ذاته دون إيجاد باقي للقسمة هو العامل المُشترك لـعددين أو أكثر.
• ومن أجل التوصل إلى العامل المُشترك الأكبر سـنتبع الخطوات البسيطة التي تم ذكرها أعلاه من أجل الوصول إلى النتيجة الصحيحة.
• فـكل عدد منهم يجب تحليله إلى عوامله الأولية عن طريق جدول الضرب.
• وبعد ذلك يتم أكبر عدد ظاهر في هذه العوامل لكل منهما، ومن خلال ذلك سـنستنتج العامل المُشترك الأكبر.

الفرق بين بين العوامل المشتركة

1_ العامل المُشترك الأكبر

أول شيء يجب إيجاد عوامل العدد، ولن نحتاج إلى تحليل العدد إلى عوامله الأولية من أجل الوصول للعامل المُشترك الأكبر.

بل يكفي إدراج العوامل المُتعارف عليها لكل عدد، ومن ثَم نبدأ في المقارنة والتفريق بين كلا المجموعتين من العوامل والقيام بتحديد الرقم الأكبر المُتكرر في كل منهما.

2_ المضاعف المُشترك الأصغر

نقوم باستنتاج المُضاعف المُشترك الأصغر لكل من الأعداد الطبيعية من خلال استخدام طريقتين:

1_ الطريقة الأولى

كتابة المُضاعفات الخاصة بكل عدد عن طريق ضرب العدد الموجود في رقم (1)، ثم ضربه في رقم (2).

ثم ضربه في رقم (3) وهكذا، ولكن تحتاج هذه العملية الكثير من الوقت والجهد من أجل التوصُّل إلى المُضاعف المُشترك الأصغر.

2_ الطريقة الثانية

استنتاج المُضاعف المُشترك الأصغر عن طريق تحليل كل الأعداد إلى عوامل أولية، ثم يتم ضربها ببعضها حسب تكراراتها.

أمثلة على إيجاد العامل المشترك الأكبر

هذه طريقة شرح العامل المشترك الأكبر بين عددين:

1 _المثال الأول: استنتج العامل المشترك الأكبر بين العددين: 12، 16؟

الحل:

استنتاج عوامل كل من الأعداد كما يلي:

ما هي عوامل العدد 12: 1، 2، 3، 4، 6، 12.

وعوامل العدد 16: 1، 2، 4، 8، 16.

نجد أن  العوامل المُشتركة بين العددين هي: (1، 2، 4).

وبذلك نستنتج أن العامل المُشترك الأكبر بين هذه العوامل المشتركة هو (4)، إذًا العامل المشترك الأكبر سيكون (4).

2_المثال الثاني: استنتج العامل المشترك الأكبر بين العددين: 10، 15؟

الحل:

استنتاج عوامل كل من الأعداد كما يلي:

• عوامل العدد 10: 1، 2، 5، 10.
• وعوامل العدد 15: 1، 3، 5، 15.
• نجد أن العوامل المشتركة بين العددين هي: (5,1).
• وبذلك يكون العامل المُشترك الأكبر بين هذه العوامل المشتركة هو (5).

3_ المثال الثالث: استنتج العامل المُشترك الأكبر بين العددين: 72، و40؟

الحل:

استنتاج عوامل كل من الأعداد كما يلي:

• عوامل العدد 72: 1، 2، 3، 4، 6، 8، 9، 12، 18، 24، 36، 72.
• وعوامل العدد 40: 1، 2، 4، 5، 8، 10، 20، 40.
• إذًا العوامل المشتركة بين العددين هي: (1، 2، 4،8)
• وبذلك نستنتج أن العامل المُشترك الأكبر بين هذه العوامل المشتركة هو (8).
  استنتاج العامل المشترك الأكبر بين ثلاثة أعداد.

1_ المثال الأول: استنتج القاسم المشترك الأكبر بين الأعداد: 18، 24، 36؟

الحل:

استنتاج عوامل كل من الأعداد الثلاثة كما يلي:

ما هي عوامل العدد 18: 1، 2، 3، 6، 9، 18.

وعوامل العدد 24: 1، 2، 3، 4، 6، 8، 12، 24.

بالإضافة عوامل العدد 36: 1، 2، 3، 4، 6، 9، 12، 18، 36.

ونجد العوامل المشتركة بين هذه الأعداد، هي: (1، 2، 3، 6).

وبما أن أكبر هذه العوامل المشتركة هو (6)، إذًا العامل المُشترك الأكبر يساوي (6).

2_ المثال الثاني: استنتج العامل المشترك الأكبر بين الأعداد: 15، 30، 105؟

الحل:

استنتاج عوامل كل من الأعداد الثلاثة كما يل:

• ما هي عوامل العدد 15: 1، 3، 5، 15.
• و عوامل العدد 30: 1، 2، 3، 5، 6، 10، 15، 30.
• عوامل العدد 105: 1، 3، 5، 7، 15، 21، 35، 105.
• نجد أن العوامل المشتركة هي: (1، 3، 5، 15).
• وبما أن أكبر عدد بين هذه العوامل المشتركة هو (15)، إذًا هو العامل المُشترك الأكبر.

3_ المثال الثالث: استنتج العامل المشترك الأكبر بين الأعداد: 180، 225، 270.

الحل:

استنتاج عوامل كل من الأعداد كما يلي:

• ما هي عوامل العدد 180: 1، 2، 3، 4، 5، 6، 9، 10، 12، 15، 18، 20، 30، 36، 45، 60، 90، 180.
• وعوامل العدد 225: 1، 3، 5، 9، 15، 25، 45، 75، 225.
• بالإضافة إلى عوامل العدد 270: 1، 2، 3، 5، 6، 9، 10، 15، 18، 27، 30، 45، 54، 90، 135، 270
• نجد أن العوامل المشتركة بين هذه الأعداد هي: (1، 3، 5، 9، 15، 45).
• وبما أن أكبر هذه العوامل المشتركة هو (45)، إذًا العامل المُشترك الأكبر يساوي (45).

ما هو الفرق بين المضاعف المشترك الأصغر والعامل المشترك الأكبر

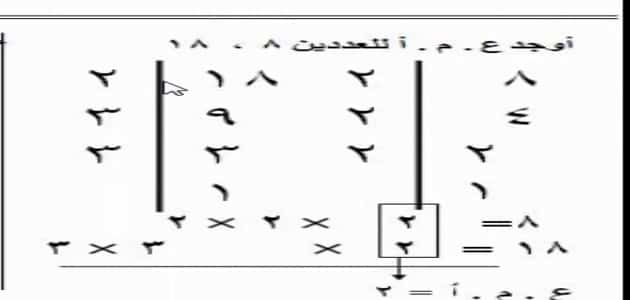
1_ المثال الأول: أوجد العامل المُشترك الأكبر للعديدين 12 و15

الحل:

في البداية سـنقوم بالبحث عن العوامل الأولية لكل من العددين 12 و15 كالآتي:

• العوامل الأولية للعدد 12 = 3 × 2 × 2.
• العوامل الأولية للعدد 15 = 3 × 5.

وبالخطوة الثانية سـنقوم باستخراج العوامل والأعداد المُشتركة بين عوامل 12 و15.

وبالتالي سـنجد أن العامل (3) هو العامل المُشترك فقط، إذًا سـنستنتج أن العامل المُشترك الأكبر هو (3).

2_ المثال الثاني: قم بإيجاد المُضاعف المشترك الأصغر للعددين 12 و15.

الحل:

في البداية سـنقوم بـكتابة المُضاعفات للعددين 12 و15 كالآتي:

• العدد 12 مضاعفاته هي: 12، 24، 36، 48، 60، 72، 84، و… وهكذا.
• والعدد 15 مضاعفاته هي : 15، 30، 45، 60، 75، 90، 10… وهكذا.
• وبالخطوة الثانية سـنقوم بإيجاد العامل المُشترك الأصغر بين الرقمين 12 و15.
• وبالتالي سـنجد أن العدد المشترك الأصغر هو (60).

التفريق بين العامل المشترك الأكبر والمضاعف المشترك الأصغر

• العامل المشترك الأكبر يكون ناتج ضرب العوامل المُشتركة الخاصة بعددين أو أكثر، والتي لديها أس أصغر.
• بينما المضاعف المُشترك الأصغر هو ناتج ضرب العوامل المشتركة للعددين وغير المشتركة أيضًا والتي لديها الأس الأكبر.

طريقة شرح العامل المشترك الأكبر، الكثير ممن يدرسون الرياضيات يستصعبون درس العامل المُشترك الأكبر، ولكنه بسيط للغاية، وهذا المقال سـيساعدك على فهمه بشكل جيد.