قانون محيط ومساحة المربع
تعد الرياضيات من أهم العلوم التي يعتمد عليها الإنسان في حياته اليومية، فهي تعتبر لغة العصر الحديث ولا يمكن الاستغناء عنها في العديد من المجالات المختلفة، ومن أهم المفاهيم الرياضية التي تمثل أساسًا في تعلم الرياضيات هي المفاهيم الهندسية ومن بين هذه المفاهيم الهندسية الأساسية هي مفهوم المربع.
ومن المفاهيم الأساسية التي ترتبط بالمربع هو قانون محيط ومساحة المربع، والذي يعتبر من أولى المفاهيم التي يتم تعلمها في الرياضيات.
محتويات المقال
قانون المربع
لا شك في أن فهم هذا القانون الرياضي الأساسي سيساعد على فهم العديد من المفاهيم الرياضية الأخرى، كما يمكن استخدام هذا القانون في الحياة العملية والحياة اليومية مثل حساب مساحة ومحيط الأراضي، وقياس المساحات في المنازل والمكاتب والمتاجر.
في هذا المقال سنتحدث عن قانون محيط ومساحة المربع وأهميته في الرياضيات والحياة اليومية وسنقدم شرحًا مفصلًا لهذا المفهوم الرياضي الأساسي بما في ذلك تعريف المربع وكيفية حساب محيطه ومساحته.
اقرأ أيضا: مساحة المربع وطول القطر
تعريف مساحة المربع
المساحة في الهندسة هي القياس الذي يشير إلى مقدار السطح الذي يشغله شكل ثنائي الأبعاد مثل المثلث أو المربع أو المستطيل وغيرها، وبالنسبة للمربع فإن مساحته هي الناتج من ضرب طول أي ضلع في طول الضلع الآخر، أو بإمكاننا استخدام الصيغة A = s^2 لحساب مساحة المربع، حيث “A” هي المساحة و “s” هو طول أي ضلع.
تعريف محيط المربع
يُعرف محيط المربع بأنه المسافة التي تحيط بالشكل الهندسي المربع، وهو يمثل إجمالي الأضلاع التي تشكل المربع ويمكن حسابه بالجمع بين طول الضلع في أربعة أضعاف، ويتم تعبير عنه بوحدة الطول المناسبة كما في المليمتر أو السنتيمتر أو الأقدام، على سبيل المثال إذا كان طول ضلع المربع يساوي 5 سم، فإن محيطه يساوي 20 سم (5 × 4).
قانون محيط ومساحة المربع
يتم دراسة المربع كشكل هندسي في مادة الرياضيات في الصف الخامس، ويعد المربع من الأشكال الهندسية الأساسية التي تتميز بأن لديها زوايا قائمة وأضلاع متساوية الطول، حيث أن تحديد:
قانون مساحة المربع
هو عبارة عن ضرب طول أي ضلع في نفسه، أي:
مساحة المربع = ضلع المربع × ضلع المربع.
قانون محيط المربع
أما قانون محيط المربع فهو عبارة عن جمع أطوال الأضلاع الأربعة، حيث تكون جميع أضلاع المربع متساوية الطول، أي:
محيط المربع = الضلع × 4.
ويعتبر المربع شكل هندسي مهم وشائع الاستخدام في الحياة اليومية، حيث يستخدم في العديد من المجالات مثل الهندسة والهندسة المعمارية والرسم الفني والتصميم الجرافيكي والكثير من التطبيقات الأخرى.
خصائص المربع
المربع هو شكل هندسي يتميز بعدة خصائص، وهي:
- جميع أضلاعه متساوية الطول: يتميز المربع بأن جميع أضلاعه متساوية الطول، وهي خاصية تميزه عن باقي الأشكال الهندسية.
- جميع زواياه متساوية القياس: تتسم زوايا المربع بأنها جميعها متساوية القياس وتساوي 90 درجة.
- المحيط: يتميز المربع بأن محيطه يساوي ضعف أي ضلع، أي إذا كان طول ضلع المربع = س، فإن محيطه يساوي 4 × س.
- المساحة: يتميز المربع بأن مساحته تساوي مربع طول أي ضلع، أي إذا كان طول ضلع المربع = س، فإن مساحته يساوي س × س أو س^2.
- القطر: يمكن حساب القطر في المربع بالرجوع إلى نقطة وسطه، حيث يمر القطر في هذه النقطة ويمثل الخط الذي يربط نقطتين متقابلتين على حافة المربع.
- التربيع: يعتبر المربع نوعًا خاصًا من التربيع، حيث يتميز بخصائصه المحددة التي سبق ذكرها.
يمكن استخدام المربع في العديد من المجالات، منها الهندسة والرياضيات والفيزياء والعمارة والتصميم، ويعد من الأشكال الهندسية الأساسية التي يتم دراستها في المدارس والجامعات.
أمثلة على مساحة المربع
يُمكن إعطاء العديد من الأمثلة على مساحة المربع، ومن هذه الأمثلة:
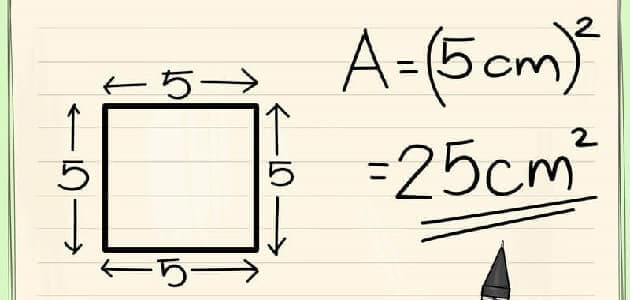
- إذا كان طول ضلع المربع يساوي 5 سم، فإن مساحته تساوي 25 سم².
- إذا كان طول ضلع المربع يساوي 3.5 سم، فإن مساحته تساوي 12.25 سم².
- إذا كان طول ضلع المربع يساوي 10 متر، فإن مساحته تساوي 100 متر².
- إذا كان طول ضلع المربع يساوي 8 بوصة، فإن مساحته تساوي 64 بوصة².
- إذا كان طول ضلع المربع يساوي 2.5 كيلومتر، فإن مساحته تساوي 6.25 كيلومتر².
وتُظهر هذه الأمثلة كيف يُمكن استخدام قانون حساب مساحة المربع لحساب المساحة بسهولة وذلك باستخدام طول ضلع المربع المعطى في السؤال.
كما أدعوك للتعرف على: المساحة الجانبية لمتوازي المستطيلات
أمثلة على محيط المربع
بالطبع! إليك بعض الأمثلة على محيط المربع:
- لو كان طول ضلع المربع يساوي 5 سم، فإن محيطه سيكون: محيط المربع = 4 × طول الضلع = 4 × 5 = 20 سم.
- إذا كانت قيمة محيط المربع تساوي 24 سم، فإن طول ضلع المربع سيكون:
- محيط المربع = 4 × طول الضلع.
- 24 = 4 × طول الضلع.
- طول الضلع = 6 سم.
- لو كان محيط المربع يساوي 36 م، فإن طول ضلع المربع سيكون:
- محيط المربع = 4 × طول الضلع.
- 36 = 4 × طول الضلع.
- طول الضلع = 9 م.
- إذا كان لديك مربع بمحيط 12 سم، فما هي مساحته؟
- محيط المربع = 4 × طول الضلع.
- 12 = 4 × طول الضلع.
- طول الضلع = 3 سم.
- مساحة المربع = طول الضلع × طول الضلع = 3 × 3 = 9 سم مربع.
- لو كانت مساحة المربع تساوي 25 سم مربع، فإن طول ضلع المربع سيكون:
- مساحة المربع = طول الضلع × طول الضلع
- 25 = طول الضلع × طول الضلع
- طول الضلع = 5 سم
- محيط المربع = 4 × طول الضلع = 4 × 5 = 20 سم
كما يمكنكم الاطلاع على: مساحة متوازي المستطيلات ومحيطه
بهذا نكون قد انتهينا من موضوع قانون محيط ومساحة المربع حيث قدمنا تعريفاً للمربع وخصائصه وشرحنا بالتفصيل قانون محيط المربع وكيفية حسابه وتطبيقاته العملية، كما تطرقنا إلى قانون مساحة المربع وكيفية حسابه وتطبيقاته في الحياة اليومية.