أولويات العمليات الحسابية في الرياضيات

أولويات العمليات الحسابية في الرياضيات، إذا طُلب منك تبسيط شيء مثل “4 + 2 × 3″، فإن السؤال الذي يطرح نفسه بشكل طبيعي هو: ما هي الطريقة التي أفعل بها هذا؟ لأن هناك خياران!

حيث يمكنني أن أضيف أولاً فتصبح النتيجة: 4 + 2 × 3 = (4 + 2) × 3 = 6 × 3 = 18، أو يمكنني الضرب أولاً فتصبح النتيجة: 4 + 2 × 3 = 4 + (2 × 3) = 4 + 6 = 10، فما هو الجواب الصحيح؟ تابعوا موقع مقال للتعرف على أولويات العمليات الحسابية في الرياضيات.

أولويات العمليات الحسابية

يبدو أن الإجابة تعتمد على الطريقة التي تنظر بها إلى المشكلة، لكن لا يمكن أن يكون لدينا هذا النوع من المرونة في الرياضيات.

فلن تعمل الرياضيات إذا لم تكن متأكدًا من الإجابة، أو إذا كان من الممكن حساب نفس التعبير بالضبط.

حتى تتمكن من الوصول إلى إجابتين مختلفتين أو أكثر بشرط اتفاقهما في النتيجة.

وللقضاء على هذا الالتباس، لدينا بعض قواعد الأسبقية أو الأولوية، والتي تأسست على الأقل منذ القرن السادس عشر.

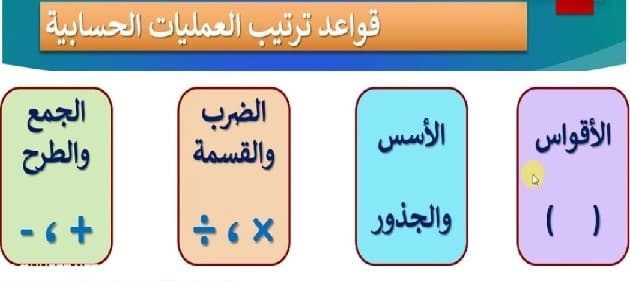
وهي التي تعرف باسم “ترتيب العمليات”، وهذه العمليات هي الجمع والطرح والضرب، والقسمة والأس، والتجميع.

ويكون ترتيب هذه العمليات كالآتي: “الأقواس، الأس، الضرب والقسمة، الجمع والطرح”.

ويمكن وصف ذلك من خلال: تفوق الأقواس الأسس، التي تتفوق على الضرب والقسمة (لكن الضرب، والقسمة في نفس الترتيب).

والضرب والقسمة يفوقان الجمع والطرح، (وهما معًا في الترتيب السفلي)، وبمعنى آخر، الأسبقية هي:

• الأقواس (تبسيط الأرقام داخل القوس).
• الأس.
• الضرب والقسمة (من اليمين إلى اليسار عندما تكون الأرقام عربية، ومن اليسار إلى اليمين عندما تكون الأرقام إنجليزية).
• الجمع والطرح (من اليمين إلى اليسار عندما تكون الأرقام عربية، ومن اليسار إلى اليمين عندما تكون الأرقام إنجليزية).

تابع أيضًا: ما هي الاعداد النسبية في الرياضيات؟

اتجاه حل المسائل

عندما يكون لديك مجموعة من العمليات من نفس الرتبة، فأنت تعمل من اليسار إلى اليمين.

على سبيل المثال، “15 ÷ 3 × 4” ليست “(15 ÷ 3) × 4 = 5 × 4″، لكنها بالأحرى “15 ÷ (3 × 4) = 15 ÷ 12”.

لأنك بالانتقال من اليسار إلى اليمين، ستصل إلى أن القسمة وقعت أولاً.

إذا لم تكن متأكدًا من ذلك، فاختبره في الآلة الحاسبة الخاصة بك، والتي تمت برمجتها باستخدام التسلسل الهرمي لترتيب العمليات.

على سبيل المثال، عند كتابة التعبير أعلاه في آلة حاسبة بيانية، ستحصل على:

  20 = 15 ÷ 3 × 4

وباستخدام التسلسل الهرمي أعلاه، نرى أنه في السؤال “4 + 2 × 3” في بداية هذه المقالة.

فكان الاختيار الثاني (الذي قيمته 10) هو الإجابة الصحيحة، لأنه يتعين علينا القيام بعملية الضرب قبل القيام بعملية الجمع.

السبب في ترتيب العمليات الرياضية

تمت تسوية ترتيب العمليات من أجل منع سوء الاتصال، ولكن يمكن أن يتسبب نظام PEMDAS، في حدوث ارتباك خاص به.

ويميل بعض الطلاب أحيانًا إلى تطبيق التسلسل الهرمي كما لو أن جميع العمليات على نفس “المستوى” (الانتقال ببساطة من اليسار إلى اليمين)، ولكن غالبًا لا تكون هذه العمليات “متساوية”.

في كثير من الأحيان، يساعد حل المشكلات من الداخل إلى الخارج، بدلاً من حل المشكلات من اليسار إلى اليمين.

لأنه غالبًا ما تكون بعض أجزاء التمرين “أعمق” من الأجزاء الأخرى، وأفضل طريقة لشرح ذلك هي حل بعض الأمثلة:

• بسّط المقدار: 3² + 4

الحل: في هذا المثال، نحن في حاجة إلى تبسيط المصطلح، مع الأس قبل محاولة إضافة العدد 4، ويمكن وصف ذلك كالتالي:

13 = 9 + 4 = 3² + 4،  إذن قيمة المقدار المبسطة هي 13

مثال

• بسّط المقدار: ²(1 + 2) + 4

الحل: في هذا المثال، يجب علينا أن نبسط الأعداد التي تتواجد بداخل الأقواس أولاً، قبل أن نتمكن من تجاوز الأس.

وعندها فقط يمكننا أن نضيف بعد ذلك العدد4، ويمكن وصف ذلك كالتالي:

13 = 9 + 4 = ²(3) + 4 = ²(1 + 2) + 4،  إذن قيمة المقدار المبسطة هي 13

مثال آخر

• بسّط المقدار: ² [(1 – 2-) 1-] + 4

لا يجب أن أحاول عمل هذه الأقواس المتداخلة من اليسار إلى اليمين، وذلك لأن هذه الطريقة هي ببساطة عرضة للخطأ.

بدلاً من ذلك، سنحاول العمل من الداخل إلى الخارج، أولًا، سنقوم بتبسيط الأعداد المتواجدة، بداخل الأقواس المتعرجة.

ومن ثم سنقوم بتبسيط ما بداخل داخل الأقواس المربعة، وبعد ذلك فقط سنقوم بالعناية بالتربيع.

بعد الانتهاء من ذلك، يمكننا أخيرًا إضافة العدد 4، ويمكن وصف ذلك كالتالي:

² [(1 – 2-) 1-] + 4

²[(3-) 1-] + 4 =

²[3] + 4 =

9 + 4 =

13 =

لا توجد أهمية خاصة لاستخدام الأقواس المربعة (“[” و “]” أعلاه)، بدلاً من الأقواس.

حيث يتم استخدام الأقواس المعقوفة والأقواس المتعرجة (الأحرف “{” و “}”)، عند وجود أقواس متداخلة، كوسيلة مساعدة لتتبع الأقواس التي يتم استخدامها مع أي من الأقواس.

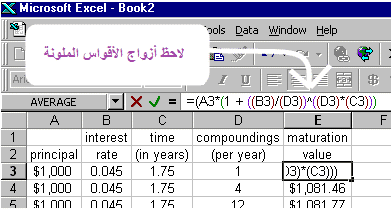
كما يتم استخدام أحرف التجميع المختلفة للراحة فقط، وهذا مشابه لما يحدث في جدول بيانات Excel عند إدخال صيغة باستخدام الأقواس:

كل مجموعة من الأقواس مشفرة بالألوان، لذا يمكنك معرفة الأزواج:

مقال

• بسّط المقدار: (4/3 + 2/3-) 4

الحل: سنقوم بتبسيط الأعداد التي تتواجد داخل الأقواس أولاً، ويمكن وصف ذلك كالتالي:

(4/3 + 2/3-) 4

أيضًا (3 / 4 + 2-) 4 =

كما أن (3 / 2) 4 =

3 / 8 =

إذن قيمة المقدار المبسطة هي 3 / 8

المشاكل المتعلقة بالتبسيط

تنبع معظم المشاكل المتعلقة بالتبسيط باستخدام ترتيب العمليات من الأقواس المتداخلة والأس وعلامات الطرح.

لذا، في الأمثلة التالية، سنقوم بشرح كيفية التعامل مع هذه الأنواع من التعبيرات.

مثال

• بسّط المقدار: 2 ÷ [(3 – 6) 2 – 4] 3 – 4

الحل: سنقوم بتبسيط المقدار من الداخل إلى الخارج: أولاً، الأقواس، ثم الأقواس المربعة، مع الحرص على تذكر أن علامة “الطرح” على 3 أمام الأقواس تتوافق مع 3.

وهذا فقط بمجرد الانتهاء من تجميع الأجزاء، سنقوم بعملية القسمة، متبوعة بجمع العدد 4، ويمكن وصف ذلك كالتالي:

2 ÷ [(3 – 6) 2 – 4] 3 – 4

2 ÷ [(3) 2 – 4] 3 – 4 =

كذلك 2 ÷ [6 – 4] 3 – 4 =

بينما 2 ÷ [2-] 3 – 4 =

كما أن 2 ÷ 6 + 4 =

وفي النهاية يساوي 3 + 4 =

7 =

إذن قيمة المقدار المبسطة هي 7

مثال آخر

• بسّط المقدار: 5 ÷ ²(3 – 8) 3 – 16

الحل: يجب أن تتذكر أنه يجب تبسيط ما بداخل الأقواس قبل أن تقوم بإجراء عملية التربيع.

لأن ²(3 – 8) تختلف عن 3² – 8² ويمكن وصف ذلك كالتالي:

5 ÷ ²(3 – 8) 3 – 16

أيضًا يساوي 5 ÷ ²(5) 3 – 16 =

5 ÷ (25) 3 – 16 =

بينما 5 ÷ 75 – 16 =

ونصل إلى 15 – 16 =

1 =

وبهذا تكون القيمة المبسطة للمقدار هي 1

اخترنا لك: ما هي الخوارزميات في الرياضيات؟

المتغيرات في العمليات الحسابية

إذا كنت قد تعلمت عن المتغيرات والجمع بين مصطلحات، فقد ترى أيضًا تمارين مثل هذه:

• بسّط المقدار: [(14x + 5 [6 – (2x + 3

الحل: إذا واجهت مشكلة في أخذ عملية طرح من خلال قوسين، فيمكنك تحويلها إلى ضرب سالب 1 في الأقواس (لاحظ اللون الأحمر المميز “1” أدناه):

[(14x + 5 [6 – (2x + 3

أيضًا [(14x + 5[6 – 1(2x + 3 =

[14x + 5[6 – 2x – 3 =

بينما يكون [14x + 5[3 – 2x =

14x + 15 – 10x =

4x + 15 =

وبهذا تكون القيمة المبسطة للمقدار هي 4x + 15

مثال

• بسّط المقدار: {2x – [3 – (4 – 3x)] + 6x} –

الحل: أنت في حاجة إلى أن تتذكر التبسيط في كل خطوة، وكذلك الجمع بين المصطلحات المتشابهة متى، وأينما يمكنك ذلك:

{2x – [3 – (4 – 3x)] + 6x} – =

كذلك 2x – 1[3 – 1(4 – 3x)] + 6x} – =

{2x – 1[3 – 4 + 3x] + 6x} – =

بينما يكون {2x – 1[– 1 + 3x] + 6x} – =

{2x + 1 – 3x + 6x} – =

أيضًا عندما {2x + 6x – 3x + 1} – =

حيث يساوي {5x + 1} – =