بحث عن المتطابقات المثلثية وإثباتها
بحث عن المتطابقات المثلثية وإثباتها، تعد المتطابقات المثلثية واحدة من أهم فروع الرياضيات والتي تختص بدراسة العلاقة بين زوايا المثلثات وأضلاعها، كما يوجد لفرع حساب المثلثات الكثير من العلاقات مع فروع الرياضيات الأُخرى، مثل علم التفاضل والتكامل والأعداد المركبة والمتسلسلات اللانهائية واللوغاريتم.
محتويات المقال
مقدمة عن المتطابقات المثلثية وإثباتها
عرف علم حساب المثلثات على أنه ذلك العلم الذي يتعامل مع العلاقة بين زوايا المثلثات والأضلاع المناظرة لها في هذه المثلثات، ومن الممكن أن يتم استخدام حساب المثلثات وتطبيقها بشكل عملي في حساب ارتفاع الكثير من المرتفعات، مثل الأشجار والجبال بتحديد ارتفاع الطائرة عن سطح الأرض والمباني، وغيرها الكثير من الأمور العملية.
شاهد أيضًا: بحث عن أخطار تواجه التنوع الحيوي وطرق المحافظة عليه
ما هو حساب المثلثات؟
- يعتبر علم حساب المثلثات أحد العلوم المتفرعة من علم الرياضيات، حيث يتناول هذا العلم الأمور المتعلقة بالمثلثات، وذلك حيث يهتم بدراسة حساب المسافة بين الأضلاع وبعضها، بالإضافة إلى التعرف على قياس الزوايا المختلفة في المثلث.
- ويعتبر علم المثلثات من الفروع المفيدة للغاية، حيث يتم استخدامه في الكثير من الفروع الأخرى للعلم، مثل الهندسة، والتطبيقات الإلكترونية، وغيرها من الفروع الأخرى.
- كما يرتبط علم حساب المثلثات بالدوال التي تختص بالزوايا، المتمثلة في جيب الزاوية، وجيب تمام الزاوية، وظل الزاوية.
ما مفهوم المتطابقات المثلثية؟
المتطابقات المثلثية أو المعادلات المثلثية يتم تعريفها على أنها عبارة عن متطابقات تتكون من مجموعة من الدوال المثلثية، وتعتبر هذه المتطابقات ذات أهمية كبيرة جدًا، حيث يتم استخدامها في حل المعادلات الرياضية وخاصة في معكوس الدالة.
تعريف المثلث
يعتبر المثلث هو من أهم الأشكال الهندسية في علم الجبر والهندسة، فهذا المثلث لديه تكوين مختلف عن أي شكل آخر وهو يتكون من رأس المثلث وضلعين آخرين، وذلك الشكل تصبح زواياه 180 درجة، وهناك 3 أنواع للمثلث ( مثلثات متساوية الأضلاع – متساوية الساقين – قائمة الزوايا).
تطابق المثلثات
يوجد مجموعة من الحالات التي تتطابق فيها المثلثات أي تكون المثلثات متشابه أو متساوية في الأضلاع المتناظرة أو الزوايا المتناظرة متساوية أيضًا أو كليهما ومن حالات تطابق المثلثات ما يلي:
- إذا كان هناك ثلاثة أضلاع في مثلث ما تتساوى مع مثلث آخر في القياس، وبالتالي تساوي الزوايا المناظرة لهذه الأضلاع في كل من المثلثين، فإننا في هذه الحالة نستطيع ان نقول ان المثلثين في حالة تطابق.
- إذا كان هناك زاوية معروفة القياس والضلعين المجاورين لها في المثلثين، فتكون الزاوية المناظرة لها في المثلث الآخر ونفس الأضلاع متساوية لها في القياس في المثلث الآخر، وفي هذه الحالة نستطيع أن نقول ان المثلثين في حالة تطابق.
- إذا كان هناك زاويتين وضلع في مثلث متساوي في القياس مع زاويتين وضلع متناظرين في مثلث آخر، وفي هذه الحالة، فإننا نستطيع أن نقول أن المثلثين في حالة تطابق.
شاهد أيضًا: بحث عن الزوايا والمستقيمات المتوازية في الرياضيات
أنواع المتطابقات المثلثية وإثباتها
هناك مجموعة من المتطابقات المثلثية الموجودة بصفة أساسية ومن أهم أنواع هذه المتطابقات المثلثية ما يلي:
متطابقات ناتج القسمة
تضم متطابقات ناتج القسمة المتطابقات التالية:
- ضا ص = جا س ÷ جتا ص، حيث أن ظا تشير إلي ظل الزاوية، وجاء تشير إلى جيب الزاوية، و جتا تشير إلى جيب تمام الزاوية، وص تشير إلى الزاوية.
- قتا ص = جتا س ÷ جا س، حيث أن قتا تشير إلى قاطع تمام الزاوية.
- متطابقات مقلوب العدد
- تضم متطابقات مقلوب العدد المتطابقات التالية: –
- قتا ص= 1÷ جا س، قا س = 1÷ جتا ص، حيث أن قا تشير إلى قاطع الزاوية، بينما تشير قتا إلى قاطع تمام الزاوية.
- ظتا ص =1÷ ظا ص، حيث أن ظتا تشير إلى ظل تمام الزاوية.
- متطابقات فيثاغورس
- تضم متطابقات فيثاغورس المتطابقة التالية: –
- جتا2 ص+ جا2 ص = 1 قا2 ص -ظا2 ص= 1 قتا 2 ص -ظتا2 ص= 1
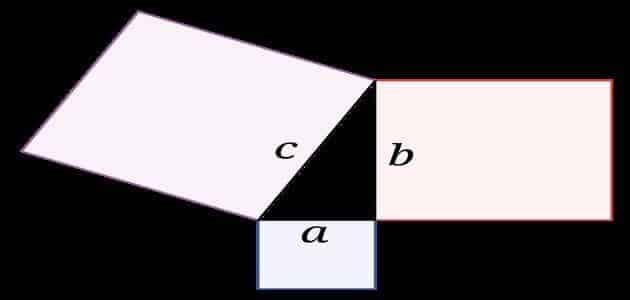
نظرية فيثاغورس
- تعتبر نظرية فيثاغورث واحدة من أشهر النظريات التي تم وضعها في علم المثلثات، حيث يتم استخدام هذه النظرية في التعرف على طول الوتر الذي يقابل الزاوية القائمة في المثلث.
- وتعتمد هذه النظرية على أن مربع طول الوتر يساوي مربع طول الضلع الأول ويضاف إليه مربع طول الضلع الثاني، ويتم استخدام قانون فيثاغورس بشكل رياضي من خلال:
- مربع طول الوتر = مربع طول الضلع الأول في المثلث + مربع طول الضلع الثاني في المثلث القائمة الزاوية.
- كما يمكن أن يتم تطبيق نظرية فيثاغورس بشكل عكسي، ففي حالة كان مربع طول الضلع الأكبر يساوي مربع أحد أضلاع المثلث مضاف إلى مربع طول الضلع الآخر، فإن المثلث يكون قائمة الزاوية.
أهم التطبيقات الحياتية على علم المثلثات
يوجد العديد من التطبيقات التي يتم فيها استخدام علم المثلثات والاستفادة من قواعده، وأهم هذه التطبيقات:
- علم الفلك: يتم استخدام علم المثلثات في التعرف على حساب المسافة التي تقع بين الشمس وكوكب الأرض، وكذلك المسافة بين القمر والأرض، لحساب نصف قطر الأرض، والتعرف على المسافات بين الكواكب وبعضها.
- الهندسة المعمارية: يتم استخدام المثلثات في الهندسة المعمارية، حيث لا يمكن أن يتم بناء أي منزل أو مبنى دون أن يتم قياس الزوايا الموجودة في جدران المنزل، وكذلك قياس الأعمدة، حتى يتم الابتعاد على عن أي انهيار منزلي، أو تشوهات في الجدران.
- تطبيقات في الملاحة: كما يمكن استخدام المثلثات في عمليات الملاحة، حيث يتم استخدام السدس، وهي عبارة عن أداة يتم استخدامها في قياس المسافات عبر التثليث.
شاهد أيضًا: بحث عن درس المستقيمان والقاطع بالتفصيل
خاتمة عن المتطابقات المثلثية وإثباتها
تعد المتطابقات المثلثية واحدة من الفروع المفيدة والمهمة التي ثبت أهميتها في تبسيط وتسهيل الكثير من الأمور الحياتية، بجانب ما تساهم فيه في كثير من العلوم الأخرى التي تفيد الإنسان وتقدمه في كثير من المجالات.