بحث رياضيات عن القطوع الزائدة

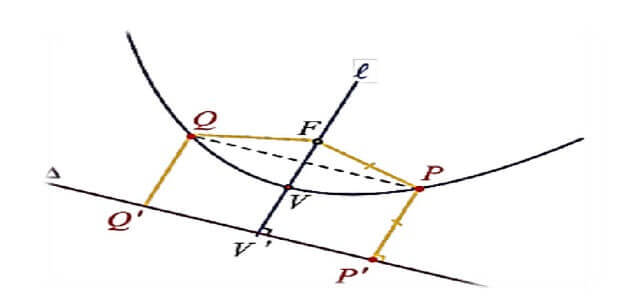
بحث رياضيات عن القطوع الزائدة، يتم تقديمه لطلاب الصفوف الثانوية ولكل من يهتم بمعرفة ماهية القطوع الزائدة ولمن يرغب في الاطلاع على مثل هذه العلوم، سوف نتعرف معكم على تساؤلاتكم حول ما يخص بحث الرياضيات عن القطوع الزائدة.

مقدمة بحث رياضيات عن القطوع الزائدة

المخروطية هي عبارة عن منحنيات تنتج عند تقاطع سطح مستوي مع مستوى مخروط ولكن بشرط ألا يمر ذلك السطح المستوي بذلك المخروط، وألا يكون متماس له وينتج عن هذا التقاطع الحادث أربعة أنواع من القطوع وهي:

• القطوع الزائدة.
• القطوع المتكافئة.
• القطوع الناقصة.
• وقد ينتج عن ذلك التقاطع المخروطي دائرة ويحدث هذا عندما يكون السطح المستوي موازياً لقاعدة المخروط.

كما يمكنك التعرف على: بحث رياضيات عن ضرب العبارات النسبية وقسمتها ثاني ثانوي

صورة عامة عن بحث رياضيات عن القطوع الزائدة

• كما أنه من الممكن أن يكون التقاطع في نقطة أو خط مستقيم.
• بالطبع سنتعرف على هذه الحالات الشاذة التي تنتج عن تقاطع المستوى والمخروط، من خلال مقالنا وأيضاً سنتعرف بشكل مفصل عن القطوع الزائدة.
• حيث سوف يتضمن المقال خواص القطوع الزائدة والاستخدامات التي من الممكن أن تستعمل فيها مثل هذه القطوع.
• ولأن القطوع الزائدة تكون من ضمن أنواع القطوع المخروطية، فكان علينا أن نتطرق إلى تعريف القطوع المخروطية قبل الشروع في معرفة ماهية القطع الزائد في بحثنا هذا.

بحث رياضيات عن القطوع الزائدة

• هناك الكثير من القطوع التي قد تنتج عن تقاطع سطح مستوي مع مخروط وذلك التقاطع الحادث يكون له عدد من الشروط.
• وسوف يشتمل في هذا الصدد عن التخصيص بالتعرف على القطوع الزائدة وينتج هذا القطع عن قطع مخروط بشكل قائم باتجاه الرأس ويكون مائل المستوى على المستوى الدالي.
• بحيث تكون الزاوية أكبر من زاوية ميل أحد تلك الرواسم على مستوى الدليل.
• وهو قطع ينتج عن تقاطع سطح مستوي لأحد نصفي مخروط بحيث يكون نسبة الاختلاف المركزي أكبر من الواحد.
• فالقطعان الزائدان يكونا مترافقين وذلك عندما يكون المحور المستعرض لأحدهما هو المحور المرافق، وعندما يكون المحور المرافق للقطع الثاني هو المحور المستعرض للآخر.
• ومن الجدير ذكره هو أن القطعان الزائدان يكونا متشابهان عندما تكون نسبة الاختلاف المركزي بينهما متساوية.

القطوع المخروطية

• فإنه هندسيا قد تم تعريف القطوع المخروطية على أنها هي ذلك المحل الهندسي لإحدى النقط المتحركة وهذا بحيث أن تكون العلاقة بين بعد النقطة المتحركة عن بعد النقطة الثابتة وبعدها عن مستقيم ثابت هي عبارة عن نسبة ثابتة.
• حيث أن النقطة الثابتة تعرف باسم البؤرة ويرمز لها بالرمز S، والخط المستقيم الثابت قد عرف باسم الدليل.
• وتكون أيضا القطوع المخروطية عبارة عن تلك الأشكال التي قد تنتج عند تقاطع سطح مستوي مع مخروطين قائمين في حالة وضع نتقابل من جهة الرأس على أن لا يمر السطح المستوي بالرأس ولا يمسه حتى فينتج عن تقاطعهما معا قطوع مخروطية.
• وقد سميت القطوع المخروطية بهذا الاسم لأنها تنشأ نتيجة تقاطع سطح المستوى مع مخروط.

ما هي أنواع القطوع المخروطية

• أنه إذا كانت نسبة الاختلاف المركزي أقل من الواحد الصحيح يسمي المنحني باسم القطع الناقص.
• فإنه قد تتكون القطوع المخروطية من تقاطع السطح المستوي والمخروط دائرة ويحدث ذلك عندما يكون الناتج عن تقاطعهما منحني مغلق.
• ويتكون المنحني المغلق نتيجة أن السطح المستوي يقطع المخروط بطريقة توازي قاعدة المخروط وتعتبر الدائرة شكل من أشكال القطوع الناقصة.
• عندما تكون نتيجة القطع بطريقة عمودية على محور تماثل المخروط ولكن بشرط أن يكون موازياً لخط واحد فقط من خطوط المخروط ويكون القطع الناتج مفتوحاً.
• وهذا يعني أن نسبة الاختلاف المركزي مساوية للواحد الصحيح ويعرف المنحني حينئذ باسم القطع المكافئ.
• أما إذا كان السطح المستوي يتقاطع مع نصفي المخروط فيتكون عن ذلك منحنين مفتوحين ويكونوا منفصلين وأنه يتم استخدام أحد المنحنيات الناتجة وإهمال الآخر.
• وتحدث هذه الحالة عندما نكون نسبة الاختلاف المركزي أكبر من الواحد الصحيح ويسمى المنحني اسم القطع الزائد.
• وتكون هناك أنواع شاذة من أنواع القطوع المخروطية الناتجة من تقاطع المخروطين المتقابلين والسطح المستوي.
• وتحدث هذه الحالة عند مرور السطح المستوي برأس المخروط.
• وذلك التقاطع يكون عبارة عن خط مستقيم عندما يمس سطح المخروط السطح المستوي، وفي حالة عندما تكون الزاوية المتكونة بين محور المخروط والسطح المستوي أكبر من المماس.

ما هي القطوع الزائدة؟

• القطع الزائد هو أحد أنواع القطوع المخروطية ويمكن أن يعرف على أنه المحل الهندسي لجميع النقاط التي تقع على السطح المستوي.
• ولكن بشرط أن تكون القيمة المطلقة للفرق ما بين بعد النقطتين عن النقطتين الثابتتين مقدار ثابت، وتسمى هذه النقطتين الثابتتين باسم البؤرتين.
• القطع الزائد يمثل منتصف المسافة بين البؤرتين.
• والمحور الذي يكون قاطعاً لسطح المستوي هو تلك القطعة المستقيمة العمودية على المحور والتي تمر بالبؤرتين.
• وأيضا فإنه يتم تكوين منحنى القطع الزائد في فرعين منفصلين وذلك لكي يحاذي كل منهما خطي التقارب.
• أما عن رأسي القطع الزائد يكونا هما النقطتين التي يتم فيهما تقاطع القطعة المستقيمة التي توصل بين البؤرتين مع فرعي المنحني.
• أما عن المحور المرافق فهو عبارة عن القطعة التي توصل بين منتصف كل من ضلعي المستطيل الموازيان لمحور القطاع.
• وتكون القطع الزائد نتيجة تقاطع المخروط مع السطح المستوي ويكونا منحنيان مفتوحان للأسفل أو للأعلى أو لليسار أو لليمين ويكون هذا وفقا لمحور التناظر للقطع.

الاختلاف المركزي

• يكون بين الأنواع المختلفة القطوع المخروطية حيث يعتمد على نقطة افتراضية F (البؤرة) ومستقيم L (الدليل) لا يمر بالنقطة F وعدد حقيقي غير ثابت مركز له بحرف e وهو معامل الاختلاف المركزي.
• فالقطعان المخروطي الذي يكون مقابل يتكون من جميع النقاط عن F مسافة مساوية ل e مرة بعدها عن L.
• فإذا كانت e=1 فأننا نحصل على قطع مكافئ، وإذا كانت e بين ال0 و1 نخلص علي قطع ناقص، أما إذا كانت e اكبر من الواحد فنحصل على قطع زائد.

ما هي استخدامات القطوع الزائدة

يتم استخدام القطوع الزائدة في الكثير من الاستخدامات والتي منها:

• يتم استخدام القطع الزائد في المجالات العسكرية، فإنه يعمل على تحديد مكان العدو من خلال تحديد مكان صوت إطلاق النار وذلك عن طريق استخدام الرادار.
• ويستخدم في بعض أنواع أنظمة الملاحة طويلة المدى ويتم استخدامه فيها والتي تعرف باسم لوران.

كيفية الحصول على القطع الزائد في الهندسة الوصفية

• نحصل عليه عن طريق قطع مخروط دوراني مركز له بالرمز K بمستوى موازي لأثنين من رأس السطح.
• أما أنها فتكون محل هندسي لمراكز الدوائر الماسة دائرتين تكونان معلومتين وفي ظل ظروف تكون فيها تلك الدائرتين متقاطعتين أو خارجتين عن بعضهما البعض لا ألا تكونان متداخلتان.
• وأيضا أن يكون نصف قطرها مختلف. أما في الحالة التي يكون فيها تساوي بين الدائرتين يكون المحل الهندسي الناتج مكون من نقاط تنتمي إلى خط مستقيم ينطبق مع محور تماثل الدائرتين.
• وبشكل عام يكون القطعان الزائدان متشابهان، إذا كان اختلافها المركزيين متساويين.

اقرأ أيضا للتعرف على: بحث عن الزوايا والمستقيمات المتوازية في الرياضيات

خاتمة بحث رياضيات عن القطوع الزائدة

في نهاية بحث رياضيات عن القطوع الزائدة نكون قد تعرفنا على القطوع المخروطية الزائدة، وقدمنا معلومات شاملة حول بحث رياضيات عن القطوع الزائدة وتعرفنا على ماهية القطوع الزائدة وعلى أهم الاستخدامات للقطع الزائد.