بحث عن ميل المستقيم اول ثانوي مقررات
بحث عن ميل المستقيم أول ثانوي مقررات، الميل هو عبارة عن أحد المفاهيم والمصطلحات المهمة في كافة فروع الرياضيات مثل الجبر والهندسة، ويساعد ميل الخط المستقيم في تحديد ومعرفة اتجاه الخط المستقيم على المحورين السيني والصادي، ويعبر أيضًا عن مدى انحراف الخط المستقيم، كما يعبر عن الفرق في الموقع بين أي نقطتين يتواجدان على الخط المستقيم، تعتبر قيمة الميل النسبة بين حركة النقطة على المحور السيني والمحور الصادي.
محتويات المقال
مقدمة عن ميل المستقيم أول ثانوي مقررات
ميل الخط المستقيم يمثل النسبة بين التغير الحادث بين كل من المحور الرأسي والمحور الأفقي، ومن ضمن الحالات التي يتواجد عليها ميل الخط المستقيم هو أن يكون رقم موجب ويشير ذلك إلى أن زيادة التغير الرأسي تؤدي إلي زيادة التغير الأفقي ولكن عندما يكون رقم سالب.
حيث يشير ذلك إلى التفكير الرأسي يقل بزيادة التغير الأفقي، ولكن عندما يكون الميل يساوي صفر فذلك يشير إلى أن المستقيم لا يحدث به أي تغير رأسي، أي أنه مستقيم أفقي ويكون المستقيم رأسي في حالة ما إذا كان ميل الخط المستقيم غير معرف وذلك نتيجة تساوي ميل المقام لصفر.
شاهد أيضًا: بحث عن درس المستقيمان والقاطع بالتفصيل
ما مفهوم ميل المستقيم؟
يمكن تعريف الخط المستقيم على أنه عبارة عن عدد من النقاط التي يكون لها ميل ثابت ومحدد ما بين أي نقطتين تقعان على هذا الخط.
وغالبا ما يتم تحديد ميل الخط المستقيم عن طريق تحديد أو معرفة قيمة نسبة التغير بين كل من التغير الأفقي إلى التغير الرأسي أو التغير العمودي، ويطلق على ميل الخط المستقيم أيضًا في العادة على أنه عبارة عن انحدار الخط الذي يصل بين أي نقطتين.
كما يمكن تعريف ميل الخط المستقيم أيضًا على أنه الخط الذي يوازي محور السينات المعروف بأنه الذي يقع على الخط الأفقي، وفي هذه الحالة فإن قيمة ميل المستقيم تساوي الصفر.
كما يتم تعريف ميل الخط المستقيم أيضًا على انه الخط الذي يوازي محور الصادات المعروف بأنه المحور الذي يقع على الخط الرأسي أو العمودي، وفي هذه الحالة دائمًا ما تكون قيمة ميل المستقيم قيمة غير معروفة، وفي الغالب ما يمتلك هذان الخطان المتوازيان ميل متساوي، ويكون ميل الخط المستقيم هو ناتج حاصل ضرب ميلي الخطين المتعامدين.
قانون ميل المستقيم
- يتم تعريف الخط المستقيم على أنه عبارة عن عدد لا نهائي من النقاط التي تقع عليها، ولكن عن القيام بإجراء عملية حسابية على الخط المستقيم للتعرف على الميل الخاص به.
- فإنه حينها لا تكون هناك حاجة إلى تحديد ومعرفة كل تلك النقاط التي تقع على الخط المستقيم، ولكن من الممكن أن يتم الاكتفاء بمعرفة وتحديد عدد أي نقطتين تقعان على نفس الخط المستقيم الذي يجب تحديد ميله.
- في حالة القيام بتحديد نقطتين ومن ثم القيام بتوصيلها ببعض عن طريق خط مستقيم، فإن هذا الخط المرسوم يسمى بالخط المستقيم، ولكن ميل الخط المستقيم يمكن تحديده ومعرفته عن طريق معرفة كل من المستوى الإحداثي السيني و المستوى الإحداثي الصادي لكل خط مستقيم يكون بإمكانه المرور بين تلك النقطتين المحددتين.
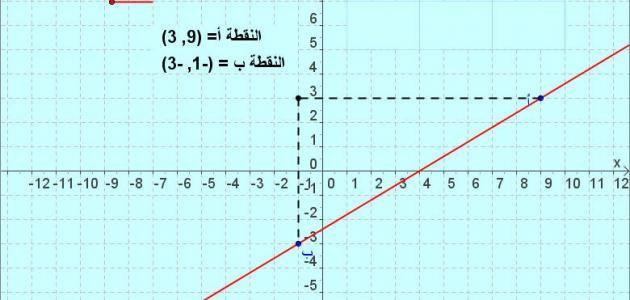
- أما بالنسبة لقانون حساب ميل الخط المستقيم فهو عبارة عن الفرق بين نقاط الإحداثي السيني ونقاط الإحداثي الصادي، ولكن هناك شرط وهو يساوي الإحداثي السيني مع الإحداثي الصادي ويتم ترجمة هذا الكلام على شكل معادلة رياضية يتم من خلالها حساب ميل الخط المستقيم وهي كالتالي
- م= (ص2-ص1) /(س2-س1).
حالات ميل المستقيم
يوجد أكثر من حالة من الممكن أن يتواجد عليها ميل الخط المستقيم فمن الممكن أن يكون ميل الخط المستقيم موجب أو قد يكون سالب أو قد يكون الميل يساوي صفر.
كما أنه من الممكن أيضًا أن يكون ميل الخط المستقيم غير معرف وتعد كل حالة لها إشارة خاصة على حالة المستقيم، حيث يتوقف ذلك على نقاط الإحداثي السيني والصادي ومن حالات ميل المستقيم ما يلي:
شاهد أيضًا: بحث عن الزوايا والمستقيمات المتوازية في الرياضيات
الميل الموجب للمستقيم
- في حالة ما إذا كان ميل الخط المستقيم رقم موجب فإن ذلك يدل على أن التغير الرأسي يزداد بزيادة التغير الأفقي، ويكون اتجاه الخط المستقيم في هذه الحالة مع الاتجاه الموجب ويصنع مع المحور الأفقي زاوية حادة.
الميل السالب للمستقيم
- في حالة ما إذا كان ميل الخط المستقيم رقم سالب فإن ذلك يدل على التغير الرأسي يقل بزيادة التغيير، ويكون اتجاه الخط المستقيم في هذه الحالة مع الاتجاه الموجب، ولكنه يصنع مع المحور الأفقي زاوية منفرجة.
ميل المستقيم صفر
- في حالة ما إذا كان ميل الخط المستقيم يساوي الصفر، فإن ذلك يدل على أن الخط المستقيم لن يتغير رأسيًا مهما كان هناك تغير أفقيًا.
الميل غير معرف
- في حالة ما إذا كان ميل الخط المستقيم غير معروف، فإن ذلك يدل على هناك تغير في المحور الرأسي بدون حدوث أي تغير في المحور الأفقي.
ميل المستقيمين المتوازيين
في حالة ما إذا كان المستقيمان في وضع توازي فإن الميل الخاص بكل منهما يكون متساوي، ولكن يتم تحقيق الحالة السابقة في توفر الشرط التالي وهو:
أن يكون المستقيمان غير رأسيين، حيث أن كل المستقيمات الراسية متوازية تبعًا للمسلمة 2.4 ويعد هذا حدث منطقي، حيث أن قيمة النسبة بين التغير الرأسي إلى التغير الأفقي تكون متساوية في حالة توازي المستقيمات، ولا ليس مهما إن كان يوجد بين المستقيمين إزالة.
ميل المستقيمين المتعامدين
في حالة ما إذا كان المستقيمان في وضع تعامد، ويكون نتيجة ذلك هو أن الميل الخاص بأحدهما هو مقلوب الميل الخاص بالمستقيم الآخر، وبالتالي يكون ناتج حاصل ضرب ميل المستقيمين المتعامدين يساوي سالب واحد
ما هي طرق إيجاد ميل الخط المستقيم؟
يوجد عدد من الطرق التي يمكن من خلالها التعرف على ميل خط المستقيم، حيث أنه من الممكن أن يتم إيجاد ميل الخط المستقيم عن طريق:
- القيام بتحديد أي نقطتين على الخط المستقيم الذي نريد معرفة الميل الخاص به، وذلك عن طريق معادلة الخط المستقيم التي يتم ترجمتها رياضيا أو القانون على النحو التالي:
- ص= (م س+ ج) حيث من خلال هذه المعادلة، فيكون ميل الخط المستقيم متمثل في معامل س الموجود في المعادلة.
- وهناك وجه آخر لمعادلة الخط المستقيم فمن الممكن أن يتم صياغتها على النحو التالي
- (أ ص+ ب س + ج = صفر) حيث من خلال هذه المعادلة فيكون ميل الخط المستقيم متمثل في ناتج قسمة معامل س علي معامل ص.
- وعن طريق تحديد كل من الأجزاء المقطوعة من المحورين السيني والصادي، ومن ثم القيام بتحويلها لنقطتين على الشكل التالي (س،0) (0، ص).
- ومن ثم بعد ذلك القيام بتطبيق قانون الميل من خلال تحديد نقطتين واقعتين على الخط المستقيم من خلال رسم الخط المستقيم بين هذين النقطتين.
شاهد أيضًا: بحث عن المتتابعات والمتسلسلات الحسابية والهندسية كامل
خاتمة عن بحث ميل المستقيم أول ثانوي مقررات
هناك الكثير والكثير من التعريفات والقوانين الموجودة في علم الجبر والهندسة والتي لا يمكن الاستغناء عنها بأي حال من الأحوال في كافة المجالات، لما لهذه القوانين من أهمية كبرى في حياتنا اليومية والعملية، ويعد ميل الخط المستقيم واحدًا من هذه القوانين الهامة.