بحث عن حالات تشابه المثلثات
بحث عن حالات تشابه المثلثات، يطلب المدرسين بحث عن حالات تشابه المثلثات من الطلاب باستمرار، حيث أن حساب المثلثات واحدة من أهم المواد الدراسية للطلاب في الصفوف الإعدادية، والتي تتناول الحديث عن كل ما يتعلق بالمثلثات سواء نظريات، قوانين، رسومات وغيرها، ونتحدث عنها بشيء من التفصيل بالمقال التالي.
محتويات المقال
تعريق المثلث وأنواعه
المثلث هو شكل 3 مغلق يتكون من 3 أضلاع، 3 رؤوس، و3 زوايا، والمجموع الكلي للزوايا يكون 180 درجة، وهناك عدة أنواع من المثلث والتي تُحدد طبقًا لقياس زواياه وطول أضلاعه وهما:
1_ متساوي الأضلاع
- يكون المثلث ذو أضلاع متساوية عندما تكون قياسات زواياه وأطوال أضلاعه واحدة، بحيث تصبح قياس الزاوية 60 درجة.
2_ قائم الزاوية
- هو عبارة عن مثلث يحتوي على زاوية عمودية أي قياسها 90 درجة.
3_ متساوي الساقين
- هو مثلث يحتوي على 2 ضلع ذو أطوال متساوية، كما تكون الزاويتان الموجودة بين قاعدتيهم متساوية.
4_ مختلف الأضلاع
- عبارة عن مثلث لا يحتوي على أيًا من زاويا أو أضلاع ذو قياسات وأطوال متساوية، وهما نوعان:
- مثلث ذو زاوية حادة أي تقل قياسها عن 90 درجة، كأن يكون قياس زاوية 70 درجة والأخرى 60 درجة والأخيرة 50 بحيث يصبح المجموع الكلي 180 درجة.
- مثلث ذو زاوية منفرجة أي تزيد قياسها عن 90 درجة كأن يكون قياس زاوية 100 درجة والأخرى 50 درجة والأخيرة 30 درجة، حتى يكون المجموع النهائي 180 درجة.
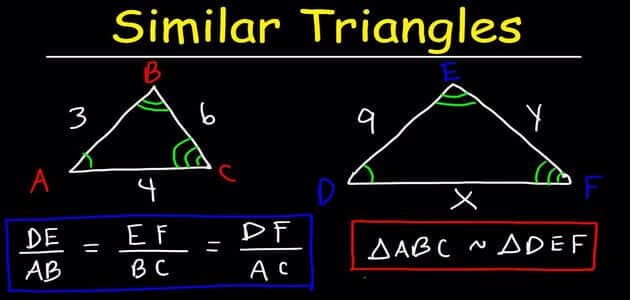
ما هو تشابه المثلثات
- يكون المثلثين متشابهين عندما تكون الزوايا المتقابلة بهما متساوية، بمعنى أنه في حالة نتج أحدهما من الأخر إما بتصغيره أو تكبيره فإن المثلثين يكونا متشابهين.
- تصبح أطوال الأضلاع بهما متناسبة أي أن النسبة تكون متساوية بين طول ضلعين المثلثين، ويتم الإشارة إلى تشابه المثلثات بذلك الرمز (~).
حالات تشابه المثلثات العامة
- يكون المثلثات متشابهات عند تناسب أطوال الأضلاع التي تكون متناظرة بهما.
- يحدث تشابه بين المثلثات في حالة تساوي قياس زاويتان داخل المثلث الـ1 مع قياس 2 زاوية داخل المثلث الـ2.
- عند تساوي زاوية في مثلث ما مع زاوية في مثلث أخر وتناسبت كذلك أطوال الأضلاع الموجودة بين تلك الزوايا فإن المثلثان متشابهين.
نتائج تشابه المثلثات
- النسبة بين كل من مساحة المثلثات المتشابهة = ( النسبة بين أي من أطوال الأضلاع المتناظرة بهما)2.
- النسبة بين كل من محيط المثلثات المتشابهة = ( النسبة بين أي من أطوال الأضلاع المتناظرة فيهما)
مثال يوضح حالة تشابه المثلثات
- إذا كان هناك مثلث أ ب ج منفرج الزاوية، وكانت هناك قطعة المستقيمة تسمى أ` ب توازي الضلع أ ب فإن المثلثين متشابهين لأن الزوايا المحصورة بين القطعة المستقيمة والضلع المتوازيان تكونا متطابقتين وتلك واحدة من حالات تشابه المثلثات.
حالات تشابه المثلثات قائمة الزاوية
بالإضافة إلى ما تم ذكره من حالات تشابه المثلثات، فإن المثلثات ذات الزوايا القائمة تشابه في الحالات التالية:
1_ بالزاوية الحادة
- عندما يكون هناك تطابق بين زاويتان حادتان في مثلثين قائمين مختلفين، فإن كل من المثلثين متشابهين.
2_ بالساق والوتر
- في حالة كون النسبة بين كل من أطوال الوترين مساوية للنسبة لأحد أطوال الساقين داخل مثلثين قائمين فهما متشابهين.
3_ بالساقين
- إذا كان هناك مثلثين قائمين وبهما ساقين متقابلين ذو أطوال متساوية، فإن كل من المثلثين متشابهين.
ولا تتردد في قراءة المزيد عبر: بحث عن تأثير اختلاف الزوايا في دقة القياسات
مجموعة من الخصائص الهامة للمثلثات المتشابهة
هناك بعض الخصائص التي تتمتع بها المثلثات المتشابه وهي:
- من الممكن معرفة أن المثلثين متشابهين بمجرد رؤية الشكل المتشابه بغض النظر عن أحجامهم.
- كل المثلثات ذات الأضلاع المتساوية تكون مثلثات متشابهة.
- في حالة كان يوجد داخل مثلثان 2 زاوية متساويين في القياس، فإن الزاوية الـ3 داخل كلاهما متساوية كذلك.
- داخل المثلثات المتشابهة تكون كل زاوية مساوية لما تقابله من زاويا.
- أي مثلث يكون مشابه لنفسه وذلك ما يطلق عليه الخاصية الانعكاسية.
- في حالة كان المثلث مشابه لمثلث أخر، فمن الطبيعي أن يكون المثلث ال2 مشابه للمثلث ال1 وتلك الخاصية تسمى بالخاصية المتناظرة.
- في حالة كان المثلث مشابه لمثلث أخر وهذا المثلث يكون مشابه لأخر فحتمًا المثلث ال1 سوف يشابه المثلث ال3 وتلك الخاصية تسمى المتعدية.
- من الممكن أن يتم استعمال خصائص تشابه المثلثات في حساب قياس أطوال الأضلاع المجهولة في أحد المثلثات.
اقرأ أيضًا من هنا: بحث عن المتتابعات والمتسلسلات الهندسية وأشكالها
أمثلة عن حالات تشابه المثلثات
من المهم التطبيق بالشكل العملي على المعلومات النظرية ولذلك نعرض الأمثلة المحلولة عن حالات تشابه المثلثات كالتالي:
1_ مثال 1
مثلثان تكون أطوال أضلاع الـ1 هي 12، 5، 2 سنتيمتر، والأخر 24، 10، 4 هل يكونا المثلثان متشابهان؟
- يتم حساب مقدار النسبة بين كل من أطوال أضلاعهما وإذا كانت واحدة فإن المثلثان متشابهين، وبالفعل عند قسمة الأطوال على بعضهما البعض ينتج رقم 2 في جميعها إذن هما متشابهين.
2_ مثال 2
مثلثين ذو زوايا قائمة ولهما أطوال سيقان متقابلة قياس كل منهم على الترتيب 7، 2 سنتيمتر 10.5، 3 سنتيمترات، هل يكونا متشابهين وكم النسبة بين قياس أطوال السيقان؟
- 5/ 7 = 1.5، و3/2= 1.5 إذن النسبة متساوية فالمثلثين متشابهين.
3_ مثال 3
مثلثين متشابهين تكون أطوال أضلاع المثلث الـ1 هي 6، 7، 8 سنتيمتر، بينما الأخر أ، ب، 6.4 سنتيمتر، فما هي قياس أطوال أضلاع الأخر؟
- بما أن كل من المثلث ال1 وال2 متشابهين إذن تكون النسبة متساوية بين قياس أطوال الساقين، 8/6.4 = 1.25.
- بالتعويض في النسبة 6/أ= 1.25 تكون أ= 4.8 سم، وعند التعويض مجددًا لإيجاد ب، 7/ب= 1.25 تكون ب= 5.6 سم.
4_ مثال 4
مثلث تكون أطوال أضلاعه على الترتيب 4، 2، 5 سنتيمتر، وأخر تكون أطوال أضلاعه 2.8، 1.4، 3.5 وتكون مقابلة لأطوال أضلاع المثلث الـ1، هل هما متشابهين؟
- عند حساب النسبة بين كل أطوال أضلاع كل من المثلثين نجد أنها متساوية = 0.7، لذا يكون المثلثين متشابهين.
5_ مثال 5
س ص ع مثلث ذو زاوية قائمة هي س وإذا كان س ه عمودي على ص ع الوتر، إذن كم مثلث متشابه ينتج في هذا الشكل.
- أولًا المثلثان س ص ع وهـ ص س يمتلكان 2 زاوية متناظرة ومتطابقة هما الزاوية س القائمة والزاوية ص إذن هما متشابهين.
- ثانيًّا المثلثان س ص ع وهـ س ع نفس الحالة السابقة إذن هما متشابهين.
- بذلك ينتج 3 مثلثات متشابهات هما س ص ع وهـ ص ع وهـ س و.
6_ مثال 6
2 مثلث متشابهين ذو زاويتين قائمتين وكان طول قاعدة المثلث الـ1 6 سم والأخر 20 سم، وكان الارتفاع 9 سنتيمتر، فما هو قياس ارتفاع المثلث الأخر؟
- بم أن كل من المثلثين متشابهين فإن النسبة بين كل من أطوال أضلاعهما سوف تكون متساوية وهي: 6/20= 3.33.
- عند التعويض بالنسبة الناتجة بين أطوال أضلاعهما يكون قياس ارتفاع المثلث الـ 2 هو 30 سنتيمتر.
كما أدعوك للتعرف على: بحث عن عالم فلك اكتشف علوم الجغرافية الفلكية
خاتمة بحث عن حالات تشابه المثلثات
في النهاية نكون بذلك قد انتهينا من شرح بحث عن حالات تشابه المثلثات للطلاب، ومن المهم التنويه على أن حساب المثلثات مادة هامة ولها أهمية في حياتنا اليومية لذا من المهم التركيز في حالات التشابه والنظريات والخصائص للتمكن من الحصول على الدرجات العليا بها.