بحث عن الإحداثيات القطبية والمركبة
بحث عن الإحداثيات القطبية والمركبة، يحتاج العديد لعمل بحث عن الإحداثيات القطبية والمركبة، وتعتبر الإحداثيات هي أرقام تعمل علي وصف المكان النسبي تقوم بدراسة منهج مادتي العلوم خصوصاً فرع الفيزياء والرياضيات ويوجد أنواع مختلفة من الإحداثيات مثل الإحداث الديكارتي.
محتويات المقال
بحث عن الإحداثيات القطبية والمركبة
قد يحتاج العديد من الأشخاص للقيام بعمل بحث عن الإحداثيات القطبية والمركبة والذي يحتاجون إليه في حياتهم العلمية، وكل بحث من هذه الأبحاث يحتاج بشكل كبير إلى العديد من العناصر لتوضيحه كالتالي:
1- الإحداثيات القطبية
- نظام الإحداثيات القطبية عبارة عن نظام إحداثيات ثنائي الأبعاد يعمل علي تحديد مكان كل نقطة داخل المستوى ذلك خلال المسافة التي تفصل كل نقطة عن مركز ما وبزاوية تكون بين المستقيم المار من المركز والنقطة نفسها.
- النظام الإحداثي عبارة عن مجموعة من المتغيرات يمكن من خلالها معرفة مكان نقطة ما داخل مستوى ثنائي الأبعاد.
- يوجد نظام إحداثي ديكارتيه يعمل علي استعمال نظام الإحداثي الكروي أو القطبي نصف القطر وزاوية المسقط داخل الدائرة الاستوائية، وزاوية المسقط على الدائرة القطبية.
- يعتبر نظام الإحداثيات القطبية هذا سهل وذلك لأنه يعبر عن العلاقة من خلال نقطتين من حيث المسافة والزاوية مثلما هو الحال داخل البندول.
2- أنواع الإحداثيات القطبية
1- الإحداثيات الأسطوانية
- تعد هي أحد الأنظمة الثلاثية الأبعاد يقوم من خلالها بتمثيل نقطة ما إلى ثلاثة رموز وهي ع، غ، ف وهي تقوم بالرمز إلى بعض المصطلحات الديكارتي وهي تعنى نصف القطر.
- الإحداثيات الأسطوانية عبارة عن المسافة بين محور الصادات والنقطة من داخل المستوي.
- الإحداثيات عبارة عن الزاوية التي تقع بين المحور والنقطة م داخل مستوى س، ص
- وتكون المسافة ذات إشارة سالبه وتوجد وسط المستوي س، ص والنقطة م.
ولا يفوتك قراءة مقالنا عن: تحليل الفرق بين مربعين في الرياضيات مع الأمثلة
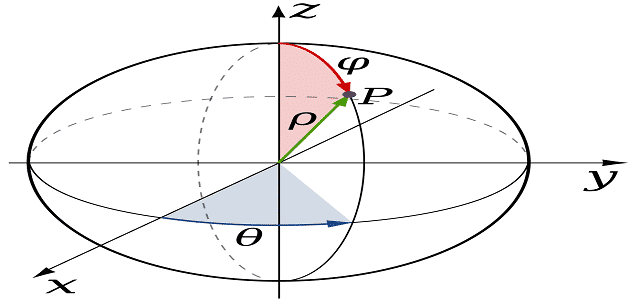
2- الإحداثيات الكروية
- هي عبارة عن نظام الإحداثيات القطبية ثلاثي الأبعاد ويتكون من نصف القطر والصادات والسمت والأوج.
3- الإحداثيات الدائرية
هو عبارة عن نظام إحداثيات ثلاثي الأبعاد يقوم بتعبير عن النقطة م من خلال ن، ت، ل.
نظام الإحداثيات ثلاثية الأبعاد
- يعمل علي توفير الأبعاد الفيزيائية الثلاث هم الطول والعرض والارتفاع، نظام الإبعاد يكون علي هيئة س، ص، ز.
- نستطيع أن نستنتج الإحداثيات النقاط س، ص، ز من خلال الأبعاد علي مستوي ص، ز وأيضاً المستوي س، ص ويمكن تقسيم النظام الثلاثي الأبعاد إلى 8 مناطق وتكون شبه مناطق ثنائية الأبعاد.
كما أدعوك للتعرف على: بحث عن المتجهات في المستوى الاحداثي
أهم الأنظمة الإحداثية ونظام الإحداثيات القطبية
أولاً نظام الإحداثيات الديكارتي
- يقوم هذا النظام علي تحديد موقع نقطة من خلال رقمين يطلق عليهم الإحداثي س والإحداثي ص ويعرف باسم مستقيم مدرج والإحداثيات تعرف باسم التفاصيل والترتيب.
- أولا نقوم بأسقاط عمودين محور سينات ومحور صادات ولابد من توحيد وحدة الطول والتدرج داخل القطاع بانتظام.
- يمكن من خلال نظام الديكارتية التعرف علي الأشكال الهندسية مثال دائرة لها شعاع مساو 2 نستطيع التعبير عنها بالمعادلة س تربيع + ص تربيع =4.
- سمي نظام الديكارتي بهذا الاسم نسبة إلى عالم الرياضيات رينية ديكارتي قام هذا العلم جهداً كبيراً على الدمج بين الجبر والهندسة.
ثانياً نظام الإحداثيات الإهليجي
- هو عبارة عن نظام إحداثيات ثنائي الأبعاد تكون فيها الإحداثيات إهليجييه ومتحدده داخل بؤرة.
ثالثاً نظام الإحداثيات الأسطوانية
- هو عبارة عن نظام إحداثيات ثلاثي الأبعاد تكون فيه نقاط الفراغ معرفة بأحداث قطبيين هم المستويات الثابتة والمسافة للقيام وإسقاطاتها المتوازية علي بعض
- من خلال المستويات والإحداثيات القطبية الأولى يطلق عليها اسم المسافة نصف القطرية أو نصف القطر.
- أما الإحداثيات القطبية الثانية يطلق عليها اسم الموضع الزاوي أو زاوية السمت أما بالنسبة للإحداثيات القطبية الثالثة فإنها يمكن الارتفاع بالطبع إذا كان المستوى المرجعي أفقي.
- أما بنسبة للخط العمودي المار على المستوى المرجعي فإنه يطلق عليه اسم المحور الطولي أو المحور الأسطواني ويمكن لهذا الخط أن يمر من مركز الإحداثيات.
- يمكن الاستفادة من نظام الإحداثيات الأسطواني عندما يرتبط بالأجسام أو الظواهر ذات التناظر الدوراني حول محور طولي.
- ويمكن الاستفادة خلال جريان الماء في داخل أنبوب مستقيم ذو مقطع عرضي مستدير.
رابعاً نظام الإحداثيات الكروية
- هو عبارة عن نظام إحداثي ثلاثي الأبعاد ويمكن من خلاله تحديد موقع النقطة من خلال 3 أعداد.
- موقع النقط هي زاوية الارتقاء أو زاوية الارتفاع للنقطة من المستوى الثابت مرورا بنقطة الأصل والمسافة الإشعاعية وهي التي تقاس من نقطة ثابتة تعرف بنقطة الأصل.
- وزاوية السمت النقطة الثالثة وهي التي تقع بين الإسقاط الموازي للخط الذي يصل بين نقطة ونقطة الأصل داخل مستوى ثابت وبين اتجاه ثابت داخل نفس المستوى.
اقرأ من هنا عن: قائمة عن أعظم علماء الرياضيات والفيزياء
تعريف الإحداثيات المركبة
- تعد الأعداد المركبة واحدة من أساسيات علم الرياضيات وهي تتكون من رقمين مركبين هم رقم أساسي لها والرقم الثاني هو العدد المركب ويطلق عليها بالرقم الخيالي للأعداد المركبة.
- يتم استخدام الأعداد المركبة في مختلف العلوم المختلفة وليس داخل علم الرياضيات فقط خصوصاً علم الجبر ويتم استخدام الأعداد المركبة في الإلكترونيات بكل أنواعها والكهرباء والديناميكا.
- الإحداثيات المركب هو الحل النهائي لمعادلة رياضية تشبه صور لبعض الأعداد منهاX^2 + a^2= 0 حيث الرمز a هو عدد حقيقي وبسب أنه عدد حقيقي يتم كتابة المعادلة هكذاx^2 = -a^2.
- في النهاية نقول إن العدد المركب هو أي عدد نستطيع أن نقوم بكتابته بالصورة ع = أ +ب ت.
الأعداد المركبة والعمليات المركبة
- باعتبار أن العنصر أ والعنصر ب هو عدد حقيقي والعنصر ت عدد جذري لسالب الواحد، أما العنصر أ بمفرده فهو يعتبر حقيقي من عدد مركب والعنصر ب هو جزء تخيلي من عدد مركب.
- نستطيع أن نعبر عن أي مجموعة أعداد مركبة بالرمز ك بالمعادلة التالية ك =ع، ع= أ+ ب ت حيث أن أ – ب تنتمي إلى لـ ح – ت= ¬جذر ال -1.
- أولاً عملية الجمع في العمليات المركبة نعبر عنها عن طريق المعادلة التالية ع1 = أ+ ب ت – وع 2 = ج + د ت.
- ونستطيع التعبير عنها خلال العلاقة التالية (أ+ ج) + (ب+ د) ت} بحيث يجب أن يؤخذ في الاعتبار أن أي عملية جمع على أي أعداد مركبة هي عملية تجميعية ومغلقة وهي أيضاً عملية تبادلية.
- تجمع الأعداد المركبة خلال عمليه الجمع بين النظير الجمعي والعنصر المحايد.
- ثانياً عملية الطرح في العمليات المركبة تنتج عن طريق المعادلة الآتية {ع1=أ+ ب ت، وع2 =ج+ د ت}.
التمثيل البياني داخل الأعداد المركبة
- أولاً يمكن كتابة العدد المركب في أي عملية تمثيل بياني بطريقة واحدة هذه الطريقة هي أ +ب ت ويمكن أن يعيين زوج مرتب من الأعداد الحقيقية.
- نستطيع تمثيل العدد (أ، ب) بنقطة على المستوى الديكارتي أو داخل المتجه الرئيسي بحيث تكون بدايته من النقطة الأصل، وينتهي بالنقطة التي تكون الإحداثيات الخاصة بها أ، ب.
- يطلق على الأعداد المركبة مسمي الإحداثي الديكارتي أو مستوى أرجاند وهذا الاسم يعود إلى العالم الفرنسي أرجند ويطلق على المحور الرأسي اسم المحور التخيلي والمحور الأفقي هو المحور الحقيقي.
نهاية المقال قد تعرفنا على العناصر التي تساعد في كتابة بحث عن الإحداثيات القطبية والمركبة ونظام الإحداثيات القطبية والمركبة وأنواع الإحداثيات القطبية والأعداد المركبة وكيفية تمثيل الأعداد المركبة بياني مع تعريف الإحداثيات المركبة.