موضوع عن الانحراف المعياري

موضوع عن الانحراف المعياري، الانحراف المعياري هو أحد مقاييس التشتت الإحصائي استخدامًا، وذلك من أجل قدرته الكبيرة، على إيجاد التبعثر الإحصائي.

حيث يعمل على إيجاد مدى الامتداد، في مجالات القيم المتواجدة بداخل مجموعة البيانات الإحصائية، ويمكنكم متابعة موقع مقال للتعرف على موضوع عن الانحراف المعياري.

ما المقصود بالانحراف المعياري؟

الانحراف المعياري هو مصطلح إحصائي، يعمل قياس تشتت مجموعة من البيانات بالنسبة إلى المتوسط.

ويتم حسابه على أنه الجذر التربيعي للتباين، ويتم حسابه على أنه الجذر التربيعي للتباين، عن طريق تحديد التباين بين كل نقطة بيانات نسبةً إلى المتوسط.

وإذا كانت نقاط البيانات أبعد من المتوسط، فسيكون هناك انحراف أعلى داخل مجموعة البيانات.

وبالتالي، كلما زاد انتشار (التشتت) البيانات، زاد الانحراف المعياري.

يتم وصف الانحراف المعياري أيضًا على أنه مقياس إحصائي في التمويل، وذلك عندما يطبق على معدل العائد السنوي للاستثمار.

والذي يعمل على إلقاء الضوء على التقلب التاريخي لهذا الاستثمار، وكلما زاد الانحراف المعياري للأوراق المالية.

وقد زاد التباين بين كل سعر والمتوسط، مما يدل على نطاق سعري أكبر.

على سبيل المثال: الأسهم المتقلبة لديها انحراف معياري مرتفع، في حين أن انحراف الأسهم الممتازة، عادة ما يكون منخفضًا إلى حد ما.

شاهد أيضًا: بحث عن التبرير الاستنتاجي في الرياضيات

ما هي الصيغة الرياضية للانحراف المعياري؟

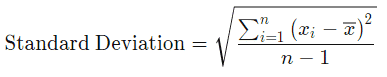
حيث أن:

• Standard Deviation = الانحراف المعياري.
• x_i = قيمة النقطة i^th في مجموعة البيانات.
• x̄ = المتوسط الحسابي لمجموعة البيانات.
• n = عدد نقاط البيانات في مجموعة البيانات.

كيف يتم حساب الانحراف المعياري؟

يتم حساب الانحراف المعياري على النحو التالي:

كما يتم حساب المتوسط الحسابي لمجموعة البيانات، وذلك عن طريق: إضافة جميع نقاط البيانات، وقسمة الناتج على عددها.

يتم حساب التباين لكل نقطة بيانات، ويتم ذلك من خلال:

1. طرح قيمة نقطة البيانات من المتوسط
2. يتم تربيع كل من هذه القيم الناتجة ويتم تلخيص النتائج
3. كما يتم بعد ذلك قسمة النتيجة، على عدد نقاط البيانات المطروح منه واحد (n-1)
   • أيضًا يتم بع ذلك أخذ الجذر التربيعي للتباين الناتج، من الخطوة الثانية أعلاه، من أجل إيجاد الانحراف المعياري.

قد يهمك أيضا: موضوع عن مقاييس التشتت

فيما يستخدم الانحراف المعياري؟

يستخدم الانحراف المعياري فيما يلي:

استراتيجيات الاستثمار والتجارة

يعد الانحراف المعياري أداة مفيدة بشكل خاص في استراتيجيات الاستثمار والتجارة.

حيث يساعد في قياس تقلبات السوق والأمن، والتنبؤ باتجاهات الأداء، بينما فيما يتعلق بالاستثمار.

على سبيل المثال، يمكن للمرء أن يتوقع أن يكون لدى صندوق المؤشر انحراف معياري منخفض مقابل مؤشره القياسي، حيث أن هدف الصندوق، هو تكرار المؤشر.

تحديد المؤشرات النسبية لدى الشركات

من ناحية أخرى، يمكن للمرء أن يتوقع أن يكون، لدى صناديق النمو القوية انحراف معياري مرتفع، عن مؤشرات الأسهم النسبية.

حيث يقوم مديرو محافظهم بالرهانات القوية لتحقيق عوائد أعلى من المتوسط، ولا يفضل بالضرورة انحراف معياري أقل.

فكل هذا يتوقف على الاستثمارات التي يقوم بها الفرد، واستعداده لتحمل المخاطر، عند التعامل مع مقدار الانحراف في محافظهم.

كما يجب على المستثمرين التفكير في تحملهم الشخصي للتقلبات، وكذلك أهدافهم الاستثمارية الشاملة.

كما أنه قد يكون المستثمرون الأكثر عدوانية مرتاحين لاستراتيجية الاستثمار التي تختارها للسيارات، ذات التقلبات الأعلى من المتوسط​​، بينما قد لا يشعر المستثمرون الأكثر تحفظًا بذلك.

قياس المخاطر الأساسية

الانحراف المعياري هو أحد مقاييس المخاطر الأساسية الرئيسية التي يستخدمها المحللون، ومديرو المحافظ الاستثمارية والمستشارون.

حيث تبلغ شركات الاستثمار عن الانحراف المعياري، لصناديقها المتبادلة ومنتجات أخرى.

ويظهر التشتت الكبير مدى انحراف العائد على الصندوق، عن العوائد العادية المتوقعة.

ونظرًا لأنها سهلة الفهم، يتم الإبلاغ، عن هذه الإحصائية بانتظام للعملاء النهائيين والمستثمرين.

قد يهمك: أنواع الإحصاء الاستدلالي التحليلي

ما الفرق بين الانحراف المعياري والتباين؟

• يتم اشتقاق التباين عن طريق أخذ متوسط ​​نقاط البيانات، وطرح المتوسط ​​من كل نقطة بيانات على حدة، وتربيع كل من هذه النتائج.
  • ثم أخذ متوسط ​​آخر لهذه المربعات، والانحراف المعياري هو الجذر التربيعي لهذا التباين.
• يساعد التباين في تحديد حجم انتشار البيانات عند مقارنتها بالقيمة المتوسطة، وكلما زاد التباين، حدث مزيد من التباين في قيم البيانات.
  • وقد تكون هناك فجوة أكبر بين قيمة بيانات وأخرى، بينما إذا كانت جميع قيم البيانات متقاربة، فسيكون التباين أصغر.
• كما يرجع صعوبة فهم هذا الأمر أكثر من الانحرافات المعيارية، بسبب الاختلافات، التي تمثل نتيجة مربعة.
  • حيث أنه قد لا يتم التعبير عنها بشكل ذي مغزى، على نفس الرسم البياني لمجموعة البيانات الأصلية.
• عادة ما تكون الانحرافات المعيارية أسهل للتصوير والتطبيق، كما يتم التعبير عن الانحراف المعياري، في نفس وحدة القياس مثل البيانات، وهو ليس بالضرورة حالة التباين.
• بالإضافة إلى ذلك فإنه باستخدام الانحراف المعياري، يمكن للإحصائيين تحديد ما إذا كانت البيانات تحتوي على منحنى عادي أو علاقة رياضية أخرى.
  • وإذا تصرفت البيانات في منحنى عادي، فستقع 68٪ من نقاط البيانات، ضمن انحراف معياري واحد للمتوسط ​، أو نقطة بيانات متوسطة.
• بينما تؤدي التباينات الأكبر إلى سقوط المزيد، من نقاط البيانات خارج الانحراف المعياري.
  • كما تؤدي التباينات الأصغر، إلى المزيد من البيانات القريبة من المتوسط.

ما هي عيوب استخدام الانحراف المعياري؟

أكبر عيب في استخدام الانحراف المعياري، هو أنه يمكن أن يتأثر بالقيم المتطرفة، حيث يفترض الانحراف المعياري التوزيع الطبيعي.

ويقوم باعتبار كل شيء له علاقة بعدم اليقين على أنه مخاطرة، حتى عندما يكون في صالح المستثمر، مثل متوسط العوائد أعلاه.

أمثلة على الانحراف المعياري

لنفترض أن لدينا نقاط البيانات 5 و 7 و 3 و 7، والتي يبلغ مجموعها 22، ثم تقوم بعد ذلك بقسمة 22، على عدد نقاط البيانات.

وفي هذه الحالة، أربع نقاط، مما ينتج عنه متوسط قيمته 5.5، وهذا يؤدي إلى القرارات التالية: x̄ = 5.5 وn = 4.

يتم تحديد التباين بطرح قيمة المتوسط ​​من كل نقطة بيانات، مما ينتج عنه القيم: 0.5- و1.5 و2.5- و1.5.

ثم يتم تربيع كل من هذه القيم، مما يؤدي إلى 0.25 و2.25 و6.25 و2.25

ثم يتم جمع القيم المربعة معًا، مما ينتج القيمة 11، والتي يتم قسمتها بعد ذلك على قيمة n ناقص 1 (n-1)، والتي تعطي القيمة 3، مما يؤدي إلى تباين يساوي، حوالي 3.67 تقريبًا.

يتم بعد ذلك حساب الجذر التربيعي للتباين، مما ينتج عنه قيمة الانحراف المعياري، والذي يساوي في هذا المثال 1.915 تقريبًا.

مثال آخر، خذ بعين الاعتبار حصص شركة آبل (AAPPL) للسنوات الخمس الماضية، حيث بلغت نسبة عائدات سهم آبل %37.7 لعام 2014.

و4.6- % لعام 2015، و10% لعام 2016، و46.1% لعام 2017، و6.8- % لعام 2018، وهنا يبلغ متوسط ​​العائد على مدى السنوات الخمس 16.5%.

قيمة عائد كل عام أقل من المتوسط 21.2%، 21.2- %، 6.5- %، 29.6%، 23.3- %، ثم يتم تربيع كل هذه القيم للحصول على: 449.4 و449.4 و42.3 و876.2 و542.9

ومن ثم تكون قيمة التباين هي 590.1، حيث يتم جمع القيم المربعة معًا، وتقسيمها على 4 (n-1)، يتم أخذ الجذر التربيعي للتباين، للحصول على الانحراف المعياري، والذي يساوي 24.3% تقريبًا.

اقرأ أيضًا: مقاييس النزعة المركزية للصف الثاني متوسط

 كان هذا موضوع عن موضوع عن الانحراف المعياري، فنرجو أن يكون هذا المقال قد أفادكم، وحاز على إعجابكم، وإذا أردتم المزيد من المصطلحات الرياضية والعلاقات الرياضية الأخرى، يمكنكم زيارة موقع مقال، حيث يتواجد قسم يختص بكل ما يتعلق بعلم الرياضيات.