موضوع تعبير عن محيط المثلث

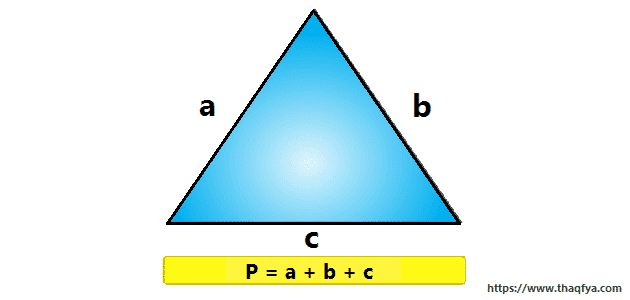
كما موضوع تعبير عن محيط المثلث، إن من أبسط الطرق للعثور على محيط المثلث، هي جمع أطوال جميع أضلاعه، ولكن، ماذا إذا كنت لا تعرف جميع أطوال الأضلاع؟ في هذه الحالة ستحتاج إلى حسابها أولاً.

وهذا يأتي دورنا في هذه المقالة، حيث ستعلمك هذه المقالة كيفية العثور على محيط المثلث، عندما تعرف أطوال الأضلاع الثلاثة، أو إذا كنت لا تعرف ذلك، فتابعوا موقع مقال للتعرف على تعبير عن محيط المثلث.

ما هو المثلث؟

المثلث هو واحدًا من أكثر الأشكال الهندسية شهرة، وهو يتكون من ثلاثة أضلاع  وثلاثة زوايا وثلاثة رؤوس.

وبعضها قد يكون متماثلاً، يتم إعطاء أضلاع المثلث أسماء خاصة في حالة المثلث القائم، ويطلق على الجانب المقابل للزاوية القائمة الوتر، ويعرف الجانبان الآخران بالساقين.

جميع المثلثات تحتوي على زوايا محدبة وثنائية المركز، وهذا الجزء من المستوى المحاط بالمثلث، يسمى المثلث الداخلي، بينما الباقي هو الخارج.

تُعرف دراسة المثلثات أحيانًا باسم هندسة المثلث، وهي منطقة غنية بالهندسة، مليئة بنتائج جميلة واتصالات غير متوقعة.

في عام 1816 م، أثناء دراسة نقاط “Brocard” للمثلث، صاح “Crelle”: “إنه لأمر رائع حقًا أن يكون الشكل البسيط للغاية.

حيث أن المثلث لا ينضب في الخصائص، كم عدد الخصائص غير المعروفة لأشكال أخرى، قد لا تكون موجودة؟”.

شاهد أيضًا: قانون محيط المثلث بالرموز

الأنواع المختلفة للمثلث

لتصنيف أنواع المثلثات المختلفة، فإن هناك نوعان للتصنيف، وهما:

تصنيف المثلثات طبقًا للأضلاع

يمكن تصنيف المثلثات حسب الأضلاع على النحو التالي:

• مثلث متساوي الساقين، وفيه يكون طول ضلعان منه متساويان، بينما يختلف عنهما طول الضلع الثالث.
• أيضًا مثلث متساوي الأضلاع، وفيه يكون جميع أطوال أضلاعه متساوية.
• مثلث مختلف الأضلاع، وفيه يكون طول كل ضلع مختلف عن الأضلاع الأخرى، فهو كما سمي “مختلف الأضلاع”.

تصنيف المثلثات طبقًا للزوايا

إن تصنيف المثلثات حسب زواياها، عبارة عن قياس كل زواياه الداخلية، ويمكن تصنيف المثلثات حسب الزوايا على النحو التالي:

• مثلث حاد الزاوية، وفيه تكون جميع زواياه حادة (أقل من 90 درجة).
• أيضًا مثلث قائم الزاوية، وفيه تكون أحد زواياه قائمة (تساوي 90 درجة)، بينما الزاويتان الآخرتان حادتان.
• مثلث منفرج الزاوية، وفيه تكون إحدى زواياه منفرجة (أكبر من 90 درجة)، بينما تكون والزاويتان الآخرتان حادتان.

خصائص المثلث

يمكن تلخيص خصائص المثلث في النقاط التالية:

• المثلث له ثلاثة أضلاع، وثلاث زوايا، وثلاث رؤوس.
• كما يكون مجموع الزوايا الداخلية للمثلث دائمًا 180 درجة.
• حاصل مجموع طول ضلعين في المثلث دائمًا يكون أكبر من طول الضلع الثالث.
• يُشار إلى المثلث برؤوس P وQ وR على أنه △ PQR.

مساحة المثلث

يمكن الحصول على مساحة المثلث بثلاثة طرق مختلفة، وتختلف هذه الطرق باختلاف نوع المثلث نفسه، حيث أنه في حالة:

•  إذا كان المثلث متساوي الساقين: فإن مساحة هذا المثلث عبارة عن “نصف طول قاعدته مضروبًا في ارتفاعه”.
•  بينما إذا كان المثلث قائم الزاوية: فإن مساحة هذا المثلث عبارة عن “حاصل طول ضلعي الزاوية القائمة مقسومًا على 2”.
•  أما إذا كان المثلث متساوي الأضلاع: فإن مساحة هذا المثلث تكون عبارة عن “طول ضلع المثلث تربيع (الجزر التربيعي لـ 3 4)”.

لكن، يعتبر القانون الأول (نصف طول القاعدة مضروبًا في الارتفاع)، هو القانون العام لإيجاد مساحة أي مثلث، ولكن للقيام بذلك، يجب أن تتوفر بعض الشروط، وهي:

• أن يكون طول أحد أضلاع المثلث معروفة، ويتم اعتباره قاعدة هذا المثلث.
• كما أن يكون طول الارتفاع المواجه للقاعدة معلومًا.
• أن نكون على معرفة بأنه إذا أردنا تطبيق هذا القانون في حالة المثلث القائم الزاوية، فإن ضلعي الزاوية القائمة اللذان، يحصران الزاوية القائمة بينهما، هما قاعدة هذا المثلث وارتفاعه.

محيط المثلث

المقصود بمصطلح “محيط المثلث” هو عبارة عن المسافة المحيطة بهذا المثلث، ولإيجاد محيط المثلث.

فإنه يعني إيجاد المسافة حول المثلث؛ ولحساب محيط المثلث، فإن أبسط صورة لذلك هي جمع أطوال جميع أضلاعه.

ولكن إذا كانت هذه الأطوال مجهولة الطول، فإننا سنقوم بإيجادها أولاً، ثم نقوم بإيجاد المحيط.

وسنتعلم في هذه المقالة كيفية العثور على محيط المثلث القائم الزاوية، عندما يكون اثنان فقط من أطوال الأضلاع معروفة.

كذلك طريقة العثور على محيط أي مثلث تعرف له طولين جانبيين، وقياس الزاوية بينهما، باستخدام قانون جيب التمام، فتابعوا القراءة.

تابع أيضًا: قانون مساحة المستطيل ومحيطه بالتفصيل

إيجاد محيط المثلث عند معرفة أطوال أضلاعه الثلاثة

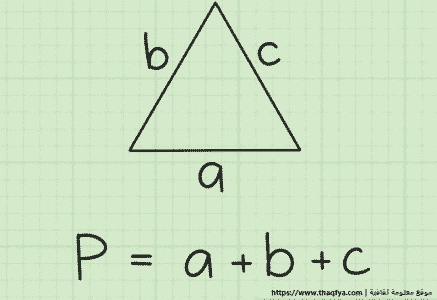
تذكر معادلة إيجاد محيط المثلث: بالنسبة للمثلث ذو الأضلاع a وb وc، يتم تعريف المحيط P على النحو التالي:

P = a + b + c

• ما تعنيه هذه الصيغة بعبارات أبسط هو أنه للعثور على محيط المثلث، ما عليك سوى جمع أطوال كل من أضلاعه الثلاثة معًا.

مثال 1

إذا كان هناك مثلث abc طول جميع أضلاعه الثلاثة هو 5 سم، فما هو محيط هذا المثلث؟

الحل: في هذا المثال، طول الضلع a يساوي 5، وطول الضلع b يساوي 5، وطول الضلع c يساوي 5.

ويسمى هذا المثال بالذات مثلث متساوي الأضلاع، حيث أن الأضلاع الثلاثة للمثلث متساوية في الطول.

لكن تذكر أن صيغة المحيط هي نفسها لأي نوع من المثلثات، وبالتالي فإن محيط هذا المثلث (p).

كما يعطى من مجموع هذه الثلاثة أضلع معًا (P = a + b + c)، أي أن: p = 5 + 5+ 5 = 15 سم.

ملحوظة

•  تذكر تضمين الوحدات في إجابتك النهائية، حيث أنه إذا تم قياس أضلاع المثلث بالسنتيمتر، فيجب أن تكون إجابتك بالسنتيمترات.
  • وإذا تم قياس الجوانب من حيث متغير مثل x، يجب أن تكون إجابتك أيضًا من حيث x.

إيجاد محيط المثلث القائم الزاوية عند معرفة طول ضلعين منه

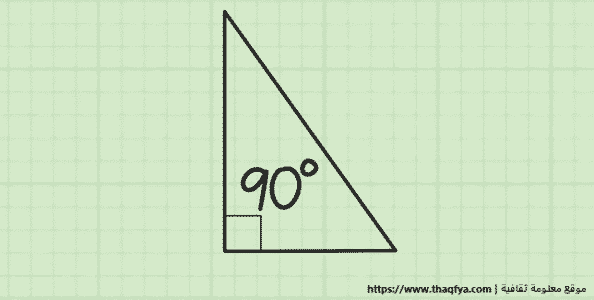
تذكر ما هو المثلث القائم الزاوية: المثلث القائم هو مثلث له زاوية واحدة قياسها “90 درجة”.

ودائمًا ما يكون ضلع المثلث المقابل للزاوية القائمة هو أطول جانب، ويسمى الوتر، تظهر المثلثات الصحيحة بشكل متكرر.

ففي اختبارات الرياضيات، ولحسن الحظ هناك صيغة مفيدة جدًا، للعثور على أطوال الأضلاع الغير معروفة.

لنفترض أن هناك مثلث أمامنا، ولنفترض تسمية أضلاعه “a” ، “b”  ،”c”، ومع تذكر أن أن أطول ضلع من هذا المثلث يسمى الوتر.

كما أنه سيكون مناظر للزاوية القائمة، سنقوم بتسميته “c”، وتسمية الأضلاع الأخرى الأقصر “a” ، “b”.

فكيف يمكن الحصول على طل أحد الأضلاع بمعلومية الضلعان الآخران؟

الإجابة هي نظرية فيثاغورس التي تخبرنا أنه بالنسبة، لأي مثلث قائم مع ضلعي a ، b، ووتر c فإن:

a² + b² = c²

وبهذا يمكننا الحصول على طول أي ضلع من المثلث القائم، بمعلومية أطوال الضلعان الآخران.

مثال 2

إذا كان هناك مثلث abc قائم الزاوية، و الضلع “c” هو الوتر، وكان طول الضلع “a” يساوي 3 سم، وطول الضلع “b” يساوي 4، فما هو محيط هذا المثلث؟

الحل: أولاً لإيجاد محيط هذا المثلث، فإننا في حاجة إلى معرفة جميع أطوال أضلاعه الثلاث.

وبما أننا معروف لدينا طول ضلعين منهما، فإنه يمكننا الحصول على طول الضلع الثالث (c)، من خلال نظرية فيثاغورث: a² + b² = c².

وبالتالي فإن:ن 

c² = 3² + 4² = 25 ، وبالتالي فإن: c = 5، أي أن طول الضلع الثالث (الوتر) يساوي 5 سم، والآن بعد أن صارت جميع أطوال الأضلاع معروفة لدينا.

فإن محيط المثلث (P = a + b + c) يعطى من العلاقة: p = 3 + 4 + 5 = 12، وبالتالي يكون محيط هذا المثلث 12 سم.

إيجاد محيط المثلث باستخدام قانون جيب التمام

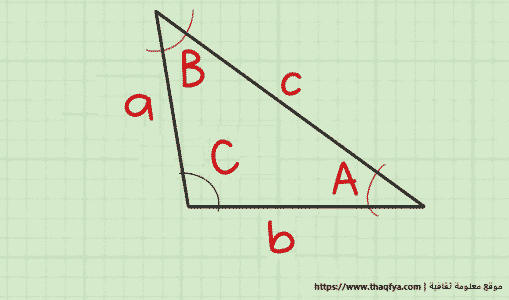
تعلّم قانون جيب التمام

يسمح لك قانون جيب التمام بحل أي مثلث عندما تعرف طول ضلعان، وقياس الزاوية بينهما.

إن هذا القانون يعمل مع أي مثلث، وهو صيغة مفيدة للغاية، وسنقوم الآن بتوضيحه، فتابعوا القراءة.

لنفترض أن هناك مثلث أمامنا، وقمنا بتعيين أحرف متغيرة لمكوناته، حيث يجب أن يتم تسمية الجانب الأول الذي تعرفه بـ “a”.

والزاوية المقابلة له هي “A”، والجانب الثاني، الذي تعرفه يجب أن يتم تسميته “b”، والزاوية المقابلة له هي “B”.

والزاوية المعلوم قياسها يجب أن تحمل علامة “C”، والجانب الثالث الذي تحتاج إلى الحصول عليه من أجل العثور على محيط المثلث.

هو الجانب “c”، فإنه يمكن الحصول على طول الضلع “c” ومن ثم إيجاد محيط المثلث، من خلال قانون جيب التمام.

وينص قانون جيب التمام على أنه بالنسبة إلى أي مثلث له أضلاع a وb وc بزاوية متقابلة A وB وC، فإن:

(c² = a² + b² – 2ab cos (C

مثال 3

إذا كان مثلث abc، طول ضلعه “a” يساوي 12 سم، وطول الضلع “b” يساوي 14 سم، وكان قياس الزاوية “C” يساوي 97 درجة، فما هو محيط هذا المثلث؟

الحل: أولاً لإيجاد محيط هذا المثلث، فإننا في حاجة إلى معرفة جميع أطوال أضلاعه الثلاث، وبما أننا معروف لدينا طول ضلعين منهما.

وقياس زاوية، فإنه يمكننا الحصول على طول الضلع الثالث (c) من خلال قانون جيب التمام:

(c² = a² + b² – 2ab cos (C.

وبالتالي فإن:

• (c² = 12² + 14² – 2 × 12 × 14 × cos (97
• كما أن (c² = 144 + 196 – (336 × -0.12187
• أيضًا (c² = 340 – (-40.95
• c² = 380.95
• c = 19.52

وبالتالي فإن طول الضلع الثالث (c) هو 16.53 سم، والآن بعد أن صارت جميع أطوال الأضلاع معروفة لدينا.

فإننا يمكننا العثور على محيط المثلث (P = a + b + c)، من خلال العلاقة: p = 12 + 14 + 19.52 = 12، وبالتالي يكون محيط هذا المثلث 45.52 سم.

اقرأ أيضًا: قانون حساب محيط نصف الدائرة

موضوع تعبير عن محيط المثلث وكل ما يتعلق بالشكل الهندسي “المثلث” ومن أجل الحصول على المزيد من المواضيع، قوموا بزيارة موقع مقال، حيث يوجد العديد والعديد من الأقسام المختلفة.