مجموع زوايا شبه المنحرف
مجموع زوايا شبه المنحرف، يعد شبه المنحرف أحد الأشكال الهندسية التي يدرسها الكثير من الطلاب في مختلف المراحل التعليمية، وفي هذا المقال سنتحدث عن مجموع زوايا شبه المنحرف، وتعريفه، وخصائصه.
محتويات المقال
تعريف شبه المنحرف
- هو شكل هندسي رباعي شبه متساوي في الساقين، وإذا تم رسم خط تناظر فإن ذلك الخط يقسم شبه المنحرف إلى زوجٍ جوانب متقابل.
- وله تعريف آخر وهو شكل هندسي رباعي الأضلاع، ويحتوي على ضلعين لهما نفس الطول ونفس قياس الزوايا
- هو شكل هندسي رباعي الأضلاع أي يحتوي على 4 أضلاع فقط، ويحتوي شبه المنحرف على ضلعين متقابلين متوازيين، أي لا يستطيعان أن يلتقيا في نقطة واحدة مهما امتدت تلك الأضلاع.
- ويضم شبه المنحرف 4 رؤوس تمثل كل رأس منها زاوية في شبه المنحرف.
- ولكل زاوية في شبه المنحرف قياس مختلف عن الأخرى ولكن لا بد أن يكون مجموع هذه الزوايا 360 درجة، مثله مثل كل الأشكال الهندسية الرباعية.
- وإذا كان ويبلغ مجموع قياس الزوايا في القاعدة العلوية الخاصة بشبه المنحرف يبلغ 180 درجة.
اقرأ من هنا عن: معلومات عن مساحة شبه المنحرف
ما هي خصائص شبه المنحرف؟
- إن شكل شبه المنحرف من الأشكال الهندسية التي لها العديد من الخصائص التي تميزها ونعرضها في السطور التالية.
- هو شكل يتكون من 4 أضلاع وكل ضلعين متقابلين في شبه المنحرف يكونان متوازيين، ويبلغ مجموع قياس زوايا شبه المنحرف المتجاورة 180 درجة، سواء أكانت الزوايا المتجاورة في القاعدة العلوية أو السفلية.
- كما يمكن حساب قيمة الخط الذي يصل بين منتصف الضلعين المتجاورين غير المتوازيين في شبه المنحرف من خلال الوسيط الذي يمثل طول الخط المتوسط ويكون طوله مساوي لطول ضلعي القاعدة المتوازيين.
- ومن خصائص شبه المنحرف أن قطريه يتقاطعان في نقطة واحدة، ومكان هذه النقطة على نفس استقامة نقطة منتصف الأضلاع المقابلة في شبه المنحرف.
ما هي أنواع شبه المنحرف؟
1- شبه المنحرف مختلف الأضلاع
- يتكون هذا الشكل من شبه المنحرف من 4 أضلاع ليست متساوية، أما قاعدتي هذا الشكل فتكونان متوازيتين، وتختلف كل واحدة منهما عن الأخرى في الطول، ويكون ساقيها غير متساويين ولا متوازيين.
2- شبه المنحرف القائم الزاوية
- يحتوي هذا النوع من شبه المنحرف على زاويتين قائمتين أي يكون مجموع قياس كل زاوية منهما يساوي 90 درجة، وتقع هذه الزاوية في قاعدة شبه المنحرف وأحد ساقيه، ولا تتقابل هذه الزوايا القائمة وإنما تكون متجاورة، ويتقاطع قطري هذا النوع من شبه المنحرف في نقطة واحدة فقط ولا يشترط أن يكون مكان هذه النقطة في منتصف شبه المنحرف.
- ويكون مجموع قياس الزاويتين المتتاليتين في هذا الشكل يساوي 180 درجة وبطريقة أخرى في القول أكثر وضوحًا يكون مجموع الزاويتين المتتاليتين على نفس الساق في شبه المنحرف يساوي 180 درجة وهذه المعلومة هامة جدًا لا بد من تذكرها جيدًا لأنك تستخدمها في الاستدلال على قياس زوايا شبه المنحرف وستتمكن من خلالها من حل الكثير من المسائل الرياضية.
3- شبه المنحرف منفرج الزاوية
- يحتوي هذا النوع من شبه المنحرف على زاوية منفرجة أي يكون قياسها أكبر من 90 درجة وتقل عن 180 درجة، تقع بين قاعدة شبه المنحرف وأحد الساقين.
4- شبه المنحرف حاد الزوايا
ويتميز هذا النوع من شبه المنحرف بأن جميع زواياه تكون حادة أي يكون قياس كل زاوية فيه أقل من 90 درجة.
5- شبه المنحرف متساوي الساقين
- ويتميز شبه المنحرف متساوي الساقين بالعديد من الخصائص ومنها.
- أول خاصية بديهية يمكن معرفتها من اسمه وهي أنه يحتوي على ضلعين متساويين في الطول.
- تساوي قطريين في شبه المنحرف متساوي الساقين.
- ويحتوي شبه المنحرف متساوي الساقين على ضلعين فقط من أصل الأربعة أضلاع متوازيين وغير متساويين.
- وتكون زاوية القاعدة في شبه المنحرف متساوي الساقين متساوية في القياس.
- ويبلغ مجموع قياس أي زاويتين متقابلين في شبه المنحرف متساوي الساقين 180 درجة.
ولا يفوتك قراءة مقالنا عن: مساحة شبه المنحرف متساوي الساقين والقائم
كيف نصل لحساب مجموع زوايا شبه المنحرف؟
- إذا أردت أن تحسب زوايا شبه المنحرف لابد أن تضع في اعتبارك معلومة أساسية تساعدك في حساب مجموع زوايا شبه المنحرف وحل المسائل الرياضية من هذا النوع.
- وهذه القاعدة هي أن مجموع أي زاويتين متتاليتين يبلغ 180 درجة.
- فمثلا إذا كان شكل شبه المنحرف المكون من زوايا س، ص، ع، ق، وكان قياس الزاوية س يساوي 100.
- إذا يكون قياس الزاوية ص التي تليها يساوي 80 درجة، طبقا للقاعدة الأساسية التي تقول إن زوايا شبه المنحرف المتتالية يساوي مجموعها 180 درجة.
أهم القوانين الخاصة بشبه المنحرف
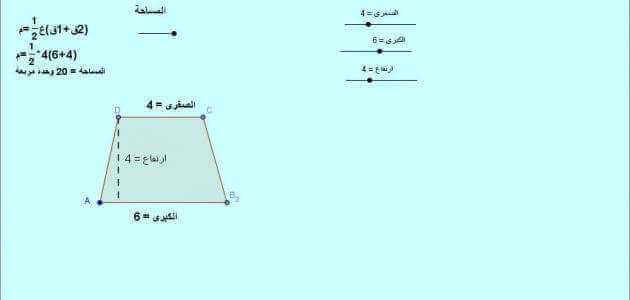
- يتم حساب مساحة شبه المنحرف ذو الزوايا القائمة، وشبه المنحرف متساوي الأضلاع والمتساوي الساقين، وشبه المنحرف العام من خلال ضرب قيمة جمع القاعدتين في الارتفاع وقيمة الناتج على الارتفاع.
- أي أن مساحة شبة المنحرف تساوي 1%2 في حاصل مجموع القاعدتين في الارتفاع.
- أما شبه المنحرف غير المنتظم يتم حساب مساحته من خلال تقسيم هذا الشكل إلى العديد من الأجزاء المعلوم مساحتها، ويتم حساب مساحة كل جزء ثم جمعهم حتى نتوصل إلى مساحة شبه المنحرف الكلية.
- أي أن مساحة شبه المنحرف = (القاعدة الكبرى + القاعدة الصغرى) × الارتفاع / 2
- ويمكن التعبير عنه من خلال الرموز الرياضية م = (ق1 + ق 2) * ع / 2
- ويمكن حساب محيط شبه المنحرف عن طريق حساب أطوال جميع الأضلاع ويكون ناتج جمعها هو محيط شبه المنحرف.
- وحين نريد أن نصل إلى قياس زوايا شبه المنحرف يمكن الاستدلال عليها من خلال خصائص شبه المنحرف.
- فمثلا إذا أردنا حساب محيط شبه المنحرف ا، ب، ج، د الذي يبلغ قياس الضلع الأول في 15 سم، والضلع الثاني 7سم، والضلع الثالث 10 سم.
- والضلع الرابع 8 سم إذا نقوم بحساب محيط شبه المنحرف عن طريق جمع أطوال الأضلاع السابقة 15+7+10+8 =40 سم إذا يساوي محيط هذا الشكل 40 سم.
- ويمثل ارتفاع شبه المنحرف أي قطعة مستقيمة تصل بين أي نقطة على ضلع في شبه المنحرف متوازي على إحدى القاعدتين إلى القاعدة الأخرى المقابلة لها.
كما يمكنك التعرف علي: مساحة المعين وشبه المنحرف
معلومات عن ارتفاع شبه المنحرف
- أولا ما هو ارتفاع شبه المنحرف؟ هو عبارة عن القطعة التي تصل بين نقطة على أحد أضلاع شبه المنحرف أي على إحدى قاعدتي شبه المنحرف وتصل بين القاعدة الأخرى المقابلة لها حتى نتمكن من عمل زاوية قائمة من خلالها.
- ونستطيع أن نقوم برسم عدد لا نهائي من هذه الخطوط المستقيمة التي تمثل ارتفاع شبه المنحرف.
- ويتم حساب ارتفاع شبه المنحرف عن طريق العديد من القوانين ومنها، أن ارتفاع شبه المنحرف يساوي حاصل ضرب 2 في مساحة شبه المنحرف ونقسمها على حاصل جمع طول قاعدتي شبه المنحرف.
- ويمكن التعبير عنه بالرموز الرياضية ع ترمز الارتفاع، م ترمز للمساحة، ق10، ق2 ترمز لقاعدتي شبه المنحرف، إذًا ع = 2 في م/ ق1+ق2.
وهكذا نكون قد قدمنا شرحًا تفصيليًا عن أهم المعلومات الخاصة بشبه المنحرف مثل تعريفه، وخصائصه، وذكرنا معلومات عن مجموع زوايا شبه المنحرف، وفي النهاية نتمنى لجميع الطلاب التفوق والنجاح.