معلومات عن مساحة شبه المنحرف
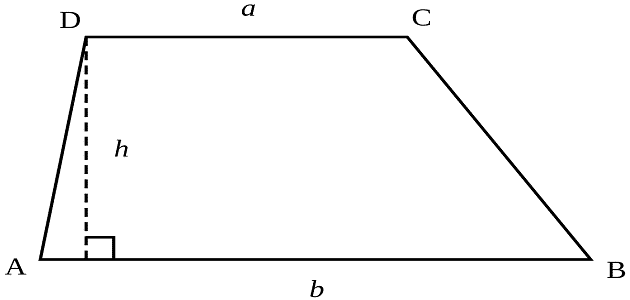
شبه المنحرف هو شكل رباعي، يوجد به ضلعان متقابلان متوازيان وهذان الضلعان يمسيان قاعدتي شبه المنحرف، أما الضلعان الآخران فهما غير متوازيين ويمثلان ساقي شبه المنحرف، ويوجد لشبه المنحرف ارتفاع وهو عبارة عن المسافة العمودية المستقيمة التي تصل بين القاعدتين.
ومن هنا يمكن القول بأن شبه المنحرف هو شكل رباعي الأضلاع ذو ضلعين متوازيين، ويمثل الضلع الأطول قاعدة شبه المنحرف السفلى، وغالبًا ما يكون طول القاعدة العليا أقصر من طول القاعدة السفلى.
محتويات المقال
أنواع شبه المنحرف
شبه المنحرف له العديد من الأنواع ومنها ما يلي:
- شبه المنحرف مختلف الأضلاع: وهذا النوع تكون فيه الأضلاع الأربعة غير متساوية، إلا أن قاعدتاه متوازيتين ومختلفتان في الطول، وساقيه غير متوازيين وغير متساويين في الطول.
- شبه المنحرف متساوي الساقين: ومن مسماه يفهم أنه يكون فيه ضلعان متساويان وهما الساقين، إلا أنهما يكونان غير متوازيتين.
- وشبه المنحرف قائم الزاوية: وهذا النوع يحتوي على زاويتين قائمتين، ودائما ما تقعان بين القاعدتين وإحدى الساقين.
- شبه المنحرف حاد الزوايا: وهذا النوع تكون زاويتاه المحصورتان بين القاعدة الأطول وبين الساقين حادة أي أقل من 90 درجة.
- شبه المنحرف منفرج الزاوية: وهو الذي يحتوي على زاوية منفرجة وتكون بين القاعدة وإحدى الساقين، والزاوية المنفرجة تعني زاوية أكبر من 90درجة وأقل من 180 درجة.
شاهد أيضًا: قانون مساحة المكعب ومحيطه
مساحة شبه المنحرف
هناك العديد من الطرق والقوانين الخاصة بحساب مساحة شبه المنحرف والتي منها ما يلي:
الطريقة الأولى: عند معرفة طول القاعدتين والارتفاع:
* مساحة شبه المنحرف = ½ × (طول القاعدة الأولى + طول القاعدة الثانية) ×الارتفاع، وبالرموز: م= ½× (أ +ب) ×ع؛ حيث أن:
- م: مساحة شبه المنحرف.
- أ: طول القاعدة السفلية.
- ب: طول القاعدة العلوية.
- ع: الارتفاع.
الطريقة الثانية: عند معرفة طول الخط المستقيم المتوسط:
* مساحة شبه المنحرف = طول الخط المتوسط ×الارتفاع.
بالرموز: م=ط ×ع، حيث:
– طول الخط المتوسط (ط) =2/ (أ +ب).
والطريقة الثالثة: استخدام صيغة هيرون:
وذلك عند معرفة أطوال جميع الأضلاع دون معرفة الارتفاع، والتي تنص على أن:
* م= ((و-أ) (و-ب) (و-أ-ج) (و-أ-د)) √× (أ +ب)/ (|أ-ب|) ، حيث أن: – م: مساحة شبه المنحرف.
- أ: طول القاعدة السفلية.
- ب: طول القاعدة العلوية.
- ج، د: طول الساقين.
- و: نصف محيط شبه المنحرف، وهو يساوي: و= (أ+ ب+ ج+ د) ÷2.
والطريقة الرابعة: عند معرفة إحدى القاعدتين:
يمكن حساب مساحة شبه المنحرف عند معرفة طول إحدى القاعدتين، والارتفاع، وطول ضلع من الأضلاع غير المتوازية، ويتم ذلك من خلال ما يلي:
- يتم تقسيم شبه المنحرف إلى مثلثين، من خلال إسقاط عمودين من زوايا القاعدة الأولى إلى القاعدة الثانية.
- يتم تطبيق نظرية فيثاغورس لكل مثلث على حدة، بهدف إيجاد طول قاعدة المثلث المجهولة من خلال القانون الآتي:(الوتر)2 = (الضلع الأول)2 + (الضلع الثاني)2.
- حساب طول القاعدة الثانية المجهولة لشبه المنحرف بجمع طول القاعدة الأولى معروفة القيمة إلى مجموع قاعدتي المثلثين.
- تطبيق معادلة مساحة شبه المنحرف: مساحة شبه المنحرف = ½ × (طول القاعدة الأولى + طول القاعدة الثانية) × الارتفاع.
خصائص شبه المنحرف
يتميز شبه المنحرف بالعديد من الخصائص والتي منها ما يلي:
- قاعدتا شبه المنحرف متوازيتان.
- يحتوي شبه المنحرف على أربعة أضلاع غير متساوية ومنهما اثنان متوازيين، واثنان غير متوازيين.
- مجموع الزوايا في شبه المنحرف 360 درجة، وهو حال أي شكل رباعي.
- يمكن إيجاد قيمة الخط المتوسط وهو الخط الواصل بين منتصف الضلعين غير المتوازيين في شبه المنحرف من خلال إيجاد الوسيط لقاعدتي شبه المنحرف، أي أن طول الخط المتوسط=طول القاعدتين المتوازيتين÷2.
- الزوايا المتجاورة في شبه المنحرف متكاملة أي مجموعها 180 درجة، ويقصد بها زوايا القاعدة العلوية، والسفلية.
- لشبه المنحرف 4 رؤوس تعرف بزوايا شبه المنحرف.
- يتقاطع قطرا شبه المنحرف في نقطة واحدة، وتلك النقطة تقع على استقامة واحدة مع نقطة المنتصف للأضلاع المقابلة.
شاهد أيضًا: معلومات عن مساحة المستطيل
خصائص شبه المنحرف متساوي الساقين
هكذا هناك بعض الخصائص التي تميز شبه المنحرف متساوي الساقين والتي منها ما يلي:
- ضلعا شبه المنحرف الغير متوازيين متساويان في الطول.
- أقطار شبه المنحرف متساوي الساقين تكون متطابقة في الطول.
- هكذا أي من زوايا القاعدة العلوية تكون زاوية متكاملة مع أي من زوايا القاعدة السفلية، وهو ما يعني أن مجموعهما = 180 درجة.
- زوايا القاعدة السفلية متطابقة، أي أنها متساوية في القياس، كما أن زوايا القاعدة العلوية متطابقة.
طريقة اشتقاق قانون مساحة شبه المنحرف
من أشهر قوانين مساحة شبه المنحرف والذي من خلاله يمكن إيجاد مساحة شبه المنحرف هو القانون الآتي:
هكذا مساحة شبه المنحرف= ½ × (مجموع طول القاعدتين) × الارتفاع.
وعن طريقة اشتقاق هذا القانون رياضيًا فهي تتم من خلال الخطوات التالية:
– تقسيم شبه المنحرف إلى مثلثين ومستطيل، وبالتالي فإن مساحة شبه المنحرف= مساحة المثلث الأول + مساحة المثلث الثاني + مساحة المستطيل، ويتم التعبير عن ذلك من خلال المعادلة التالية:
مساحة شبه المنحرف= (½) × قاعدة المثلث الأول × ارتفاعه + (½) × قاعدة المثلث الثاني × ارتفاعه + طول المستطيل × عرضه، ويمكن توضيح ذلك من خلال استخدام الرموز.
هكذا ذلك من خلال افتراض أن هناك شبه منحرف تم تقسيمه إلى مثلث أول قائم طول قاعدته “أ”، وارتفاعه “ع”، ومستطيل قاعدته “ب ” وارتفاعه “ع.
ومثلث قائم آخر قاعدته “ج” وارتفاعه “ع”، ومن ثم فإن مساحة المثلث الأول= (½)×أ× ع، ومساحة المثلث الثاني= (½)×ج× ع، ومساحة المستطيل= ب× ع.
هكذا ينتج مما سبق أن مساحة شبه المنحرف = (½)×أ× ع+(½)×ج× ع+ ب× ع، وبضرب الطرفين في2 ينتج أن 2×مساحة شبه المنحرف = أ×ع+ج×ع+2ب×ع، وبإخراج ع كعامل مشترك ينتج أن 2×مساحة شبه المنحرف = ع× (أ+ج+2ب).
ومن خلال القسمة على 2، وبمعرفة أن (أ+ ج+ ب) يساوي طول القاعدة السفلية وهو ب 2، وأن “ب ” هو طول القاعدة العلوية ينتج أن مساحة شبه المنحرف= ½ × مجموع طول القاعدتين × الارتفاع= ½ × (ب+ب 2) ×ع.
أمثلة متنوعة على حساب مساحة شبه المنحرف
المثال الأول:
شبه منحرف فيه طول القاعدة العلوية=21سم، وطول القاعدة السفلية= 31سم، وارتفاعه= 5سم، أوجد مساحته.
الحل:
هكذا من خلال تطبيق قانون مساحة شبه المنحرف= ½× (طول القاعدة الأولى+ طول القاعدة الثانية) × الارتفاع. م=½×(21+31) ×5=130سم².
المثال الثاني:
هكذا شبه منحرف، فيه مجموع طولي القاعدتين يساوي62 دسم، أما ارتفاعه فيساوي 18 دسم، احسب مساحة شبه المنحرف.
الحل:
هكذا من خلال تطبيق قانون مساحة شبه المنحرف= ½× (طول القاعدة الأولى+ طول القاعدة الثانية) × الارتفاع، ومنه مساحة شبه المنحرف=½×(62) × 18=558 دسم².
المثال الثالث:
شبه منحرف، فيه طول القاعدة الأولى=4سم، وطول القاعدة الثانية= 6سم، أما ارتفاعه= 3سم، جد مساحته.
الحل:
من خلال تطبيق قانون مساحة شبه المنحرف= ½×(طول القاعدة الأولى+ طول القاعدة الثانية)× الارتفاع.
هكذا مساحة شبه المنحرف=3×(4+6) × ½
ومساحة شبه المنحرف= 3×(10) × ½
هكذا مساحة شبه المنحرف= 3×5
إذن: مساحة شبه المنحرف= 15سم².
قوانين محيط شبه المنحرف
القانون الأول: محيط شبه المنحرف = مجموع أطوال أضلاعه.
القانون الثاني: محيط شبه المنحرف= أ+ ب+ ع×((1/جاس) + (1/جاس)).
شاهد أيضًا: موضوع تعبير عن مساحة المعين
هكذا وفي النهاية نكون قد حددنا كل ما يجب معرفته عن حساب مساحة شبه المنحرف، وقوانين المساحة وأيضًا الأنواع الخاصة به.