ما هي خواص شبه منحرف؟
ما هي خواص شبه منحرف؟، التي تميزه حيث أنه يكون قريب من متوازي الأضلاع ولكن يختلف في كون أن متوازي الأضلاع كل جانبين متقابلين متوازيين، أما الشبه منحرف قاعدتاه متوازيان وسنشرح ذلك بالتفصيل.
محتويات المقال
ما هي خواص شبه منحرف؟
- يسمى شبه المنحرف رباعي الأضلاع حيث يوجد جانبان متوازيان فقط ويسمى كل جانب السطح السفلي لشبه المنحرف.
- وهذا يختلف عن متوازي الأضلاع في متوازي الأضلاع يكون كل جانبين متقابلين متوازيين، وخاصية شبه المنحرف له الخصائص التالية: السطحان السفليان لشبه المنحرف متوازيان.
- تعني الزاوية المجاورة أن زوايا القاعدة العلوية والقاعدة السفلية لشبه المنحرف مدمجة لذلك فإن مجموعهم يصل إلى 180 درجة.
- مجموع زوايا شبه المنحرف هو 360 درجة، وهو نفس مجموع زوايا الشكل الرباعي.
- يحتوي شبه المنحرف على أربعة رؤوس تسمى الزوايا شبه المنحرفة.
- يمكن العثور على قيمة الخط الذي يربط بين الجانبين غير المتوازيين من شبه المنحرف من خلال إيجاد وسيط الضلعين السفليين من شبه المنحرف (الخط الأوسط) أي: طول الخط الأوسط = طول شبه منحرف قاعدتان متوازيتان / 2.
- يتقاطع قطري شبه المنحرف عند نقطة متصلة مع نقطة المنتصف على الجانب الآخر.
- يحتوي شبه المنحرف على أربعة جوانب غير متساوية، وكما ذكرنا من قبل: اثنان منهم متوازيان، واثنان غير متوازيين.
- شبه المنحرف متساوي الساقين له عدة خصائص وهي الأضلاع غير المتوازية من شبه المنحرف لها نفس الطول.
- زوايا القدم متشابهة أي أنها بنفس الحجم، وزوايا القاعدة العلوية هي نفسها أيضًا، قطريها متماثلان، أي الطول متساوٍ.
- أي ركن من أركان القاعدة العلوية في شبه المنحرف يعتبر عددًا صحيحًا مع أي زاوية من القاعدة السفلية؛ أي أنك بزاوية 180 درجة بالنسبة لها.
اقرأ من هنا عن: معلومات عن مساحة شبه المنحرف
محيط شبه منحرف
توجد مجموعة من القوانين لإيجاد محيط شبه منحرف، وتفسيرها كالتالي: شبه منحرف له جوانب مختلفة: أي أن أضلاعه الأربعة لها أطوال مختلفة، ويمكن إيجاد محيطها باستخدام القانون، كما يلي:
- القانون الأول: محيط شبه منحرف = مجموع أطوال الأضلاع على سبيل المثال، إذا كان هناك شبه منحرف ABCD أطوال ضلعه 4 سم و7 سم، وطول الضلع السفلي 12 سم و15 سم، يكون المحيط: المحيط = 4 + 7 + 12 + 15 ما يساوي 38 سم.
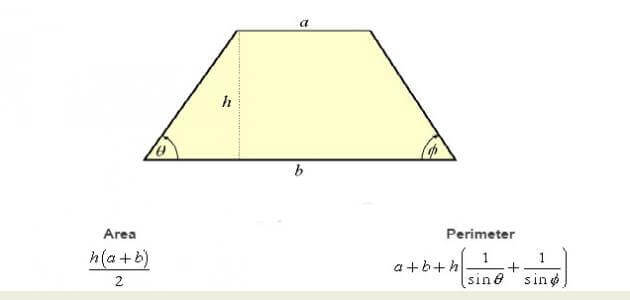
- القانون الثاني: محيط شبه المنحرف = السطح السفلي + السطح السفلي + الارتفاع × ((1 / ja الزاوية السفلية اليمنى) + (1 / ja الزاوية السفلية اليسرى)، بالرمز: شبه منحرف دائري = أ + b + hx ((1 / jas) + (1 / stucco))).
- حيث: [2] a وb: قياسات قاعدتين متوازيتين في شبه المنحرف، S: ارتفاع شبه المنحرف؛ Q: الزاوية اليمنى بين القدم والساق الأولى. R: هي الزاوية اليسرى بين القدم السفلية والساق الثانية.
- شبه المنحرف الأيمن: هو شبه منحرف يتضمن زاويتين قائمتين، ويمكن إيجاد محيط شبه المنحرف الأيمن بالعلاقة التالية: المحيط = a + z 1 + z 2 + الجذر التربيعي للقيمة (a² + (p 2-p 1) ².
- من بينها: (3) ج: طول جانب واحد من شبه المنحرف، أي جانب الزوايا القائمة على الجانب الآخر. P1، p2: طول ضلعي شبه المنحرفين المتوازيين.
- شبه منحرف متساوي الساقين: محيط شبه منحرف متساوي الساقين = أ + ب + 2 ج، حيث: أ، ب: طول القاعدة العلوية والسفلية، ج: الضلعان غير المتوازيين أو الأطوال المتساوية لشبه المنحرف (الساقين) الطول.
- على سبيل المثال: إذا كان هناك شبه منحرف متساوي الساقين يبلغ طول قاعدته العلوية وقاعدته السفلية 5 سم و10 سم، وطوله غير المتوازي متساوي الأضلاع 7 سم، فإن محيطه يكون: شبه منحرف = 5 + 10 + (2 × 7)، يساوي 29 سم.
مساحة شبه منحرف
منطقة شبه منحرف توجد مجموعة من القوانين لإيجاد الفضاء شبه المنحرف موضحة كالتالي:
القانون الأول
- استخدم الطول والارتفاع لقاعدتي شبه المنحرف، أي: مساحة شبه المنحرف = (الارتفاع / 2) (القاعدة الأولى + القاعدة الثانية)، واستخدم الرمز: شبه المنحرف = p / 2 x (s1 + s2)).
- حيث: p: ارتفاع شبه المنحرف، s2: الجزء السفلي من شبه المنحرف، ق 1: الجزء السفلي من شبه المنحرف العلوي.
- على سبيل المثال إذا كان هناك شبه منحرف يبلغ ارتفاعه 5 سم وطول قاعدته المتوازية 4 سم و10 سم، فإن مساحته هي: المساحة = (5/2) × (4 + 10)، أي ما يعادل 35 سنتيمترات مربعة.
القانون الثاني
- استخدم الأضلاع الأربعة الأطول لشبه منحرف مع عدم ارتفاعه لإيجاد المساحة وتسمى هذه الصيغة بصيغة هيرون وهي:
- مساحة شبه المنحرف = (أ + ب) / (| أ-ب |) الجذر التربيعي لقيمة x ((x-a) x (x-b) x (x-a-c) x (x-a-d))؛ حيث: أ، ب: طول الجزء العلوي والسفلي من شبه المنحرف، أ، د: طول ضلعين شبه منحرفين غير متوازيين.
- سؤال: مُعرَّف بأنه محيط شبه المنحرف يساوي: (أ + ب + ج + د) / 2.
القانون الثالث
- عندما يعرف طول الخط الأوسط وارتفاعه، يمكن التعبير عن القانون الأول على النحو التالي: مساحة شبه المنحرف = طول الخط الأوسط × الارتفاع.
- والخط الأوسط هو الخط الذي يربط بين نصفي شبه منحرف، وهو ما يساوي: الخط الأوسط = (الأول طول الضلع السفلي + طول الضلع السفلي الثاني) / 2.
- المثال الأول: ما مساحة شبه منحرف متساوي الساقين؟ القاعدة العلوية والسفلية من الترابيكولا طولها 9 سم وطولها 5 سم وليست متوازيتين، وطول أحد أضلاع متساوي الأضلاع 4 سم.
- ارتفاع شبه المنحرف مثلث قائم الزاوية بقاعدته، وزاويته السفلية 60 درجة؟، الحل: مساحة شبه المنحرف = ½ x w x (s 1 + s 2).
- من أجل إيجاد ارتفاع شبه المنحرف (الذي يشكل أيضًا ارتفاع مثلث قائم الزاوية)، يمكن استخدام قانون جيب الزاوية، أي: ja (زاوية) = الجانب المقابل / الوتر ومن هذا ja (60) = الارتفاع / 4 = 0.866، بالتالي: الارتفاع = 3√2.
- مساحة شبه المنحرف = ½ x3√2x (9 + 5)، وبالتالي فإن مساحة شبه المنحرف = 3-14 سم
ولا يفوتك قراءة مقالنا عن: مساحة شبه المنحرف متساوي الساقين والقائم
ارتفاع شبه منحرف
- يمكن تعريف ارتفاع شبه المنحرف على أنه مقطع مستقيم يربط أي نقطة على أحد الجانبين المتوازيين من شبه المنحرف بالجانب السفلي المقابل لتشكيل زاوية قائمة.
- تجدر الإشارة إلى أن شبه المنحرف يمكن أن يرسم عددًا لا يحصى من الخطوط المستقيمة للتعبير عن الارتفاع.
- هناك عدة قوانين لمعرفة ارتفاع شبه المنحرف، وهي: الارتفاع = (2 × مساحة شبه المنحرف) / (المجموع من طول القاعدتين)، بالرمز: v = (2 xm) / (q1 + q2).
- حيث m: منطقة شبه المنحرف، S1، وS2: السطح السفلي لـ شبه منحرف متوازي. P: ارتفاع شبه المنحرف. P = gx gas ، أو v = dx plaster ؛ حيث: [11] x ، y: الزاويتان السفليتان السفلية.
- C و d: هما أطوال الجانبين غير المتوازيين من شبه المنحرف اختر أحد الزوايا السفلية في حالة الزاوية يجب تحديد الجانب المجاور للركن عند استبدال القاعدة P: ارتفاع شبه منحرف.
شبه منحرف المختلف الأضلاع
- لا تتساوى جوانبه الأربعة.
- قاعدتها متوازية لكن الطول مختلف.
- الساقين ليست متوازية وغير متساوية.
شبه منحرف المتساوي الساقين
- ساقاه متساويتان ولكنهما غير متوازيين.
- وقاعدتها متوازي وغير متساوي.
كما يمكنك التعرف على: مساحة المعين وشبه المنحرف
لقد قمنا بالإجابة على سؤال ما هي خواص شبه منحرف؟ وذكر أنواع منه حيث يوجد شبه المنحرف القائم الزاوية الذي يحتوي على زاويتين قائمتين وتقع الزاويتان القائمتان بين القاعدتين.