موضوع عن قانون البعد بين نقطتين

موضوع عن قانون البعد بين نقطتين، من القوانين الرياضية الهامة والتي تستحق الدراسة باستفاضة، قانون البعد بين نقطتين، حيث أنه قانون رياضي سهل وبسيط ولكن كثير من مستخدمي القوانين الرياضية يقف أمامه في بعض النقاط.

فهو قانون يستوجب تسجيل إحداثيات النقاط التي سيتم احتساب المسافة بينهم ومن ثم تطبيق قانون البعد بين نقطتين، لذلك كان علينا شرحه بالتفصيل من خلال موضوع عن قانون البعد بين نقطتين.

ما هو قانون البعد بين نقطتين؟

• يعتبر قانون البعد بين نقطتين هو أحد القوانين الرياضية الهامة، والمستخدمة بكثرة حيث يستخدم لاحتساب المسافة بين أي نقطتين على المستوى الديكارتي.
• وتعتبر تلك المسافة التي يتم احتسابها بين نقطتين على الأرض فقط وليس الفضاء حيث أن هذا القانون يطبق على المسافة الأرضية فقط.
  • وهذه معلومة هامة يجب الانتباه لها جيدا، فإن العلماء يستخدمون السنة الضوئية لتقدير المسافة الفلكية أو المسافة بين نقطتين في الفضاء.
  • لأن سرعة الضوء ثابتة لن تتغير، أما في الهندسة الوصفية فلا يوجد قوانين رياضية لحساب المسافة بين نقطتين.
  • بل تستخدم بأساليب إسقاطيه اخرى لها قوانين أخرى لا تنطبق على المسافة بين نقطتين على الأرض.
•  يمكن حساب المسافة بين نقطتين
• (س1، ص1) والنقطة (س2، ص2) أو بمعنى آخر كلامي يحسب هذا القانون طول الخط الممتد بين نقطتين:
•  النقطة 1 والنقطة 2، حيث تعتبر المسافة الخطية هي الجذر التربيعي مربع المسافة الأفقية مضاف إليها مربع المسافة العمودية بين نقطتين وتقوم بحساب تلك المسافة من خلال الصيغة التالية:
•  المسافة 2 =
• (س2 – س1)2 + (ص2 – ص1)2
• وبالتالي فإن المسافة تساوي الجذر التربيعي ل ((س2 – س1)2 + (ص2 – ص1))2

شاهد أيضًا: موضوع عن اقليدس عالم الرياضيات

إيجاد قانون البعد بين نقطتين

يمكننا إيجاد البعد بين نقطتين من خلال تلك الخطوات التالية:

• اولًا

نقوم بتحديد إحداثيات النقطتين على المستوى الديكارتي على فرض أن النقطة الأولى تساوي أ، والنقطة الثانية تساوي ب.

• ثانياً:

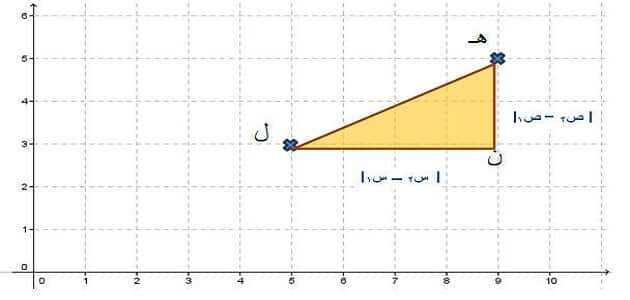
نقوم برسم خط مستقيم يصل بين النقطة أ والنقطة ب، كما تعمل على إكمال الرسم ليتكون مثلث قائم الزاوية في النقطة ج حتى يمكننا تطبيق نظرية فيثاغورس على المثلث القائم الزاوية.

• ثالثاً:

نقوم بتطبيق قانون فيثاغورس على المثلث القائم الزاوية في ج الذي نشأ من خلال الرسم، فأن من خلال نظرية فيثاغورس يتضح أن:

(ب ج) 2 + (ج أ) 2 = (أ ب) 2

• رابعاً:

نقوم بتحديد إحداثيات النقطتين أ وب، بحيث أن النقطة أ تساوي (س1، ص1) والنقطة ب تساوي

(س2، ص2)

•  ينتج أن المسافة الأفقية

(ب ج) = س1 – س2، وكذلك المسافة العمودية (ج أ) = ص1 – ص2.

• خامساً:

تعويض قيمة كل من (ب ج) و (ج أ) في الخطوة السابقة بقانون نظرية فيثاغورس فينتج ما يأتي: المسافة 2 = (س1 – س2)2 + (ص1 – ص2)2

المسافة بين النقطتين أ وب = الجذر التربيعي للقيمة ((س1 – س2)2 + (ص1 – ص2)2).

تطبيقات على قانون البعد بين نقطتين

هناك الكثير من التطبيقات والأمثلة التي يمكن أن نوضح من خلالها قانون البعد بين نقطتين لكي يتضح من خلال الأمثلة وطريقة حلها كيفية إيجاد المسافة بين نقطتين بطريقة سهلة وفي خطوات ثابتة بسيطة، مثل:

مثال 1/:

أوجد المسافة بين النقطة (1،7) والنقطة (3،2)

الحل/ :

المسافة بين نقطتين = الجذر التربيعي ل ((س2 – س1)2 + (ص2 – ص1)2) المسافة = الجذر التربيعي لـ ((1 – 3)2 + (7 – 2)2)

المسافة = الجذر التربيعي ل (4 + 25) = الجذر التربيعي ل (29).

مثال 2/:

أوجد المسافة بين النقطتين (2،3) و (5،7)

 الحل/:

المسافة بين نقطتين = الجذر التربيعي ل ((س2 – س1)2 + (ص2 – ص1)2) المسافة = الجذر التربيعي ل ((5 – 2)2 + (7 – 3)2)

المسافة = الجذر التربيعي ل (9 + 16) = الجذر التربيعي ل (25) = 5

مثال 3/:

إذا كانت إحداثيات النقطة هي

أ (1 ،3) وإحداثيات النقطة ب هي: (5 ،6)، أوجد البعد بين النقطتين أ وب.

الحل/:

(أ ب) ² = (س2 – س1)² + (ص2 -ص1)² (أب)² = (5-1)² + (6-3)²

(أب) ² = 4²+3²

و(أب) ² = 16+9=25

(أب) = 5 وحدات.

شاهد أيضًا: بحث عن الأعمدة والمسافة في الرياضيات

مثال 4/:

إذا كانت النقطة هـ تأخذ الإحداثيات (3، -5) والنقطة وتأخذ الإحداثيات (-6، -10)، أوجد البعد بين النقطتين هـ و.

الحل/:

و(هـ و) ² = (س2 – س1)² + (ص2 -ص1)² (هـ و)² = ( -6 – 3)² + ( -10 – -5)² (هـ و)² = ( -9)² + ( -5)²

(هـ و) ² = 81 + 25

و(هـ و) ² = 106

(هـ و) = جذر 106 وحدة.

ملحوظه هامه في حل مسائل إيجاد المسافة بين نقطتين

هناك ملحوظة هامة يجب الانتباه لها عند حل مسائل إيجاد المسافة بين نقطتين وهي أننا دائمًا ما نأخذ القيمة المطلقة للجذر.

لان ناتج المسافة بين نقطتين لابد أن تكون موجبة، فهي لا تحتمل أن تكون سالبة، وان الجذر التربيعي دائمًا له ناتجين أما موجب أو سالب.

لذلك يجب القيمة المطلقة الجذر حتى يكون الناتج موجب فقط، أي أن القيمة المطلقة للقانون وإشارتها (l l)، بهذا الشكل التالي:

| (أب) ² = (س2 – س1)² + (ص2 -ص1)² l .

ملحوظة هامة في حل مسائل إيجاد المسافة بين نقطتين

هناك ملحوظة مهمة يجب الانتباه لها عند حل مسائل إيجاد المسافة بين نقطتين وهي أننا دائمًا ما نأخذ القيمة المطلقة للجذر.

لأن ناتج المسافة بين نقطتين لابد من أن تكون موجبة، فهي لا تحتمل أن تكون سالبة، وان الجذر التربيعي دائمًا له ناتجان إما موجب أو سالب.

لذلك يجب القيمة المطلقة الجذر حتى يكون الناتج موجبا فقط، أي أن القيمة المطلقة للقانون وإشارتها (l l)، بهذا الشكل التالي:

| (أب) ² = (س2 – س1)² + (ص2 -ص1)² l.

خطوات إيجاد المسافة بين نقطتين

هناك خطوات يجب اتباعها عن حل مسائل إيجاد المسافة بين نقطتين، وتلك الخطوات هي:

• تسجيل إحداثيات نقطتين تريد إيجاد المسافة بينهما.
• نقوم بتسمية إحداهما نقطة
• 1 (x1, y1) والثانية 2 (x2, y2) ولا يهم في التسمية أيهما الأول وأيهما الثاني بشرط البقاء على ذلك الترتيب طوال حل المسألة.
• X1 هي الإحداثي الأفقي (على طول محور x) للنقطة 1، و x2 هي الإحداثي الأفقي للنقطة 2.
• Y1 هي الإحداثي الرأسي (على طول محور y) للنقطة 1، و y2 هي الإحداثي الرأسي للنقطة 2.
• نقوم بطرح y2 -y1 لإيجاد المسافة العمودية، ثم أطرح x2 -x1 لمعرفة المسافة الأفقية.
• لا تقلق إذا نتج عن الطرح أرقام سالبة الخطوة التالية هي تربيع هذه القيم والتربيع دائمًا ما ينتج عنه عدد صحيح موجب.
• ثم إيجاد المسافة على طول المحور y.
• ثم إيجاد المسافة على محور x.
• نقوم بتربيع كل القيم. هذا يعني أن نقوم بتربيع مسافة المحور x، (x2 x1)، وأن تربع مسافة المحور y، (y2 -y1)، كل منهما بشكل منفصل.
• ثم اجمع القيم المربعة يعطيك هذا مربع المسافة الخطية القطرية بين نقطتين.
• والخطوة الأخيرة هي أن بحساب الجذر التربيعي للمعادلة، فيكون المسافة الخطية بين النقطتين هي الجذر التربيعي لمجموع القيم المربعة لمسافة المحور x ومسافة المحور.

شاهد أيضًا: موضوع عن الهندسة الفراغية في الرياضيات

فإن موضوعنا عن قانون البعد بين نقطتين قد وضح بالتفصيل كيفية حساب البعد بين نقطتين والطريقة الرياضية لذلك، وفي النهاية، فإنه لحساب المسافة بين نقطتين يتعين.

وضع القانون والبدء في التعويض طبقًا الأرقام وإحداثيات كل نقطة كما بينا من خلال موضوع عن قانون البعد بين نقطتين.