خواص متوازي الاضلاع من حيث الزوايا
خواص متوازي الاضلاع من حيث الزوايا، هي أشكال هندسية ثنائية الأبعاد تتكون من أربعة أضلاع مستقيمة، تلتقي في نقاط معينة تسمى الرؤوس أو الزوايا لتشكل سوياً شكلاً هندسياً مغلقاً.
مجموع زواياه 360 درجة، أما بالنسبة لأهم خصائصها فلكل شكل رباعي أربع زوايا، وأربعة رؤوس، أربعة أضلاع.
محتويات المقال
متوازي الأضلاع
- هكذا متوازي الأضلاع هو أحد الأشكال الهندسية الرباعية الأضلاع؛ حيث إنه يتميز بأن له أربعة أضلاع.
- وكل ضلعان متقابلان متطابقان ومتوازيان سوياً، أو يكونان متطابقان فقط أو متوازيان فقط.
- كما أن له أربعة زوايا مجموع زواياها تصل الى 360 درجة مثل أي شكل رباعي هندسي.
- وأن قياس كل زاويتين متقابلتين في متوازي الأضلاع يكون متساوي؛ ومتوازي الأضلاع.
- هكذا يحتوي على قطرات يتقاطع كل منهما مع الآخر في منتصف الشكل وكل منهما ينصف الآخر.
- حيث أن كل قطر يصل الى بين الزاويتين المتقابلتين؛ ومن خصائص متوازي الأضلاع.
- أن كل زاويتين على ضلع واحد يكون مجموعهما 180 درجة؛ وقد يطلق على متوازي الأضلاع اسماً آخر وهو شبيه المعين.
شاهد أيضًا: خصائص المضلعات المتشابهة
الخصائص المشتركة بين متوازي الأضلاع وبين الأشكال الرباعية:
- أن مجموع قياسات زوايا متوازي الأضلاع تساوي 360 درجة.
- أن محيط متوازي الأضلاع يساوي مجموع أطوال أضلاعه.
- ويتكون متوازي الأضلاع من أربعة أضلاع.
- أن مساحة متوازي الأضلاع تساوي حاصل ضرب طول القاعدة × طول الارتفاع الساقط عليه.
خصائص متوازي الأضلاع
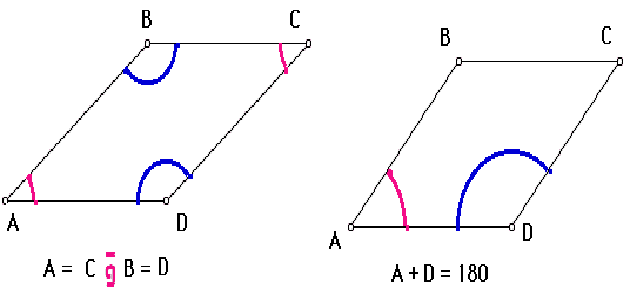
- كل زاويتان متقابلتان متساويتان.
- مجموع كل زاويتين متحالفتين “على ضلع واحد” تساوي 180 درجة.
- كل ضلعان متقابلان متساويان.
- كل ضلعان متقابلان متوازيان.
- مساحة متوازي الأضلاع تساوي ضعف مساحة المثلث المشكل بضلعان وقطر.
- كل قطر في متوازي الأضلاع ينصف للقطر الآخر.
- يتقاطع قطرا متوازي الأضلاع في نقطة تشكل مركز تناظر لمتوازي الأضلاع، وتعرف باسم مركز متوازي الأضلاع.
- أي مستقيم يمر بمركز متوازي الأضلاع يقسمه الشكلان متطابقان.
- مجموع مربعات أطوال الأضلاع يساوي مجموع مربعي طولي القطريين “وذلك هو قانون متوازي الأضلاع.
وإن تحقق في مضلع رباعي محدب واحد من الخصائص السابقة فهذا يعني أن الشكل هو متوازي أضلاع، كما أن إثبات أن ضلعان متقابلان متوازيان ومتساويان في القياس في آنٍ سوياً يثبت أن هذا الشكل متوازي أضلاع.
حالات خاصة من متوازي الأضلاع
هكذا يوجد هناك ثلاث حالات خاصة من متوازي الأضلاع، وهي المعين، والمستطيل، والمربع، وبما يأتي توضيح لكل منها:
- المستطيل: بما أن المستطيل هو متوازي أضلاع، فهو يتميز بكافة خصائص متوازي الأضلاع.
- إلا أنه يوجد بعض الخصائص التي تميزه عن متوازي الأضلاع، وتلك الخصائص هي:
أن كافة زواياه الأربعة قوائم.
وأقطاره متساوية في الطول، وتقوم بتنصيف زواياه.
- المعين: ويعرف المعين بأنه شكل رباعي يكون الأربعة أضلاع به متساوية في الطول، وكل معين هو متوازي أضلاع.
- وبما أنه متوازي أضلاع فهو يتصف بكافة خصائص متوازي الأضلاع.
- بالإضافة إلى خصائص أخرى تميزه عن متوازي الأضلاع، وتلك الخصائص هي:
كافة الأضلاع الأربعة متساوية.
هكذا أقطاره متعامدة على بعضها؛ أي أنها تشكل زاوية قياسها 90 درجة، وتنصف زواياه.
- المربع: ويعرف المربع بأنه متوازي أضلاع يمتلك كافة خصائص المعين، والمستطيل، ومن أهم وأبرز خصائصه الآتي:
- كافة أطوال أضلاع المربع متساوية في الطول كالمعين.
- زوايا المربع الأربعة قوائم كالمستطيل.
- أقطار المربع متساوية في الطول كالمستطيل.
- وأقطار المربع تعامد بعضها كالمعين.
- أقطار المربع متطابقة كالمستطيل، وتنصف زواياه.
قد يهمك: شكل متوازي المستطيلات في الرياضيات
أمثلة على خصائص متوازي الأضلاع من حيث الزوايا
المثال الأول
س/ شكل رباعي أ ب جـ د فيه قياس الزاوية أ= 3س + 9، وقياس الزاوية ب= 5س + 20، وقياس الزاوية جـ= 3س، وقياس الزاوية د= 2س + 6، فما هو قياس الزاوية د؟
الحل:
- هكذا يمكن حل تلك المسألة عن طريق معرفة قاعدة أن مجموع زوايا الشكل الرباعي التي تنص على أن “مجموع زوايا أي شكل رباعي يساوي 360 درجة”.
- وبالتالي فإن 5س+9+5س+20+3س+2س+6= 360. 13
- س+35 =360. 13
- س= 325.
- س= 25.
- وبالتالي فإن قياس الزاوية د: 2×25+6، وتساوي 56 درجة.
المثال الثاني
متوازي أضلاع د هـ و ي، قاعدته “هـ و” فيه قياس الزاوية د =2س + 12، وقياس الزاوية هـ =5س، فما هو قياس الزاوية و؟
الحل:
- هكذا يمكن حل تلك المسألة بواسطة استخدام خاصيتين من خصائص متوازي الأضلاع، وهي أن كل زاويتان متحالفتان.
- بمعنى “تقعان على ضلع واحد” يكون مجموعها 180 درجة، وفي تلك المسألة الزاوية د.
- والزاوية هـ زاويتان متجاورتان، والخاصية الأخرى أن كل زاويتان متقابلتان متساويتان، وفي تلك المسألة الزاوية د، والزاوية ومتقابلتان.
- وعليه: (2س+12) + (5س) = 180 درجة.
- 7س + 12 = 180.
- 7س = 168.
- س= 24.
- وبالتالي فإن قياس الزاوية ويساوي قياس الزاوية د، ويساوي 2 × 24 + 12، ويساوي 60 درجة.
المثال الثالث
متوازي أضلاع أ ب جـ د، قاعدته “ب ج” فيه قياس الزاوية أ= (س + 15ص) درجة، وقياس الزاوية جـ= 127 درجة، وفيه طول الضلع ب جـ = 54، وطول الضلع أد = س²+5، فما هي قيمة المتغيرين س، وص؟
الحل:
- هكذا يمكن إيجاد قيمة المتغيرين بواسطة استخدام خاصيتين من خصائص متوازي الأضلاع إحداهما أن كل زاويتان متقابلتان متساويتان فالزاوية أز
- والزاوية جـ متقابلتان، وبالتالي متساويتان، والأخرى أن كل ضلعين متقابلان متساويان فالضلع ب جـ مقابل للضلع أ د، وبالتالي يساويه.
- إيجاد قيمة س عن طريق مساواة طول الضلعان ب جـ، وأ د، وهذا كما يلي:
- س²+5=54
- س²=49، وبالتالي فإن س = 7.
- إيجاد قيمة ص عن طريق مساواة الزاويتين أ، وجـ، وهذا كما يلي:
- س + 15ص= 127
- 7 + 15ص = 127
- ص = 8
المثال الرابع
متوازي أضلاع د ع هـ و، قاعدته “ع هـ” فيه قياس الزاوية د= 5ص، وقياس الزاوية ع= 115 درجة، وقياس الزاوية هـ= (7 س – 5)، فما هي قيمة المتغيرين س، وص؟
الحل:
- هكذا يمكن حل السؤال بواسطة استخدام خاصيتين من خصائص متوازي الأضلاع، وهي أن كل زاويتان متحالفتين متكاملتان.
- أي أن مجموعها 180 درجة، وفي تلك المسألة الزاويتان د، وع متحالفتان، والزاويتان هـ، ومتحالفتان.
- والخاصية الأخرى أن كل زاويتان متقابلتين متساويتان، وفي تلك المسألة الزاوية ع، والزاوية ومتقابلتان.
- حساب قيمة ص، وهذا كما يلي:
- 5ص + 115 = 180.
- 5ص = 65.
- ص = 13.
- حساب قيمة س، وهذا كما يلي:
- 115 + (7س – 5) = 180.
- 7س + 110 = 180.
- 7س = 70.
- س = 10.
تابع أيضًا: موضوع تعبير عن حجم متوازي المستطيلات
المثال الخامس
متوازي أضلاع أ ب جـ د، وقاعدته “د ج”، فيه قياس الزاوية أ= 56 درجة، فما هو قياس زواياه الثلاثة الأخرى؟
الحل:
هكذا يمكن إيجاد الزوايا الأخرى بواسطة استخدام خصائص متوازي الأضلاع.
- من خصائص متوازي الأضلاع أن كل زاويتين متقابلتين متساويتان، والزاوية أ وجـ هما زاويتان متقابلتان، وبالتالي فهما متساويتان، وبالتالي فإن قياس الزاوية ج أيضاً= 56 درجة.
من خصائص متوازي الأضلاع أن كل زاويتين متحالفتين مجموعها= 180 درجة، والزاوية د هي زاوية متحالفة مع الزاوية أ، وبالتالي يمكن إيجاد قياسهما كما يلي:
- قياس الزاوية د: 56 + ∠ د = 180
- وبالتالي فإن الزاوية (∠) د قياسها= 124 درجة.
- الزاوية ب تقابل الزاوية د، وبالتالي فإن قياسها 124 درجة.
هكذا في هذا المقال نكون قد أوضحنا لكم خواص متوازي الأضلاع من حيث زواياه، على أمل أن يعود عليكم بالفائدة الكلية.