بحث عن حل المعادلات والمتباينات الاسية وأنواعها كاملة
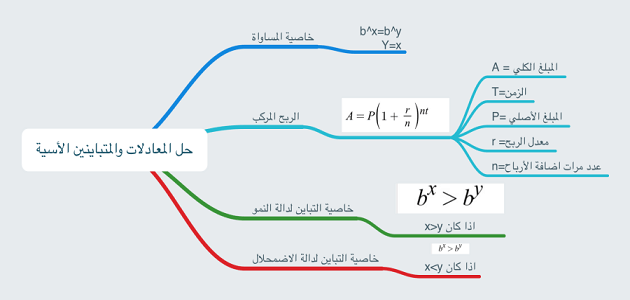
بحث عن حل المعادلات والمتباينات الاسية وأنواعها كاملة، إن حل المتباينات أو المعادلات الأسية يعتبر من المفاهيم والقوانين الأولية في علم الجبر من مادة الرياضيات.
وهي عبارة عن علاقات رياضية تتطلب في حلها المعرفة الكاملة لقوانين الدالة الأسية، وفي هذا المقال سيتم بحث عن حل المعادلات والمتباينات الاسية وأنواعها كاملة، وكذلك تبسيط مفهوم المتباينات الأسية وتوضيح طريقة حلها.
محتويات المقال
بحث عن حل المعادلات والمتباينات الاسية وأنواعها كاملة
- حل المعادلات والمتباينات الأسية يحتوي على شقين مختلفين، وهما حل المتراجحات وحل المعادلات، حيث تختلف المتباينة عن المعادلة بشكل عام من حيث الإشارات الرياضية التي تقسم بين طرفي العلاقة، ولذلك فيجب وضع المبادئ والقوانين الرياضية الخاصة بهما أمام الأعين، والتركيز على كل المكونات في طرفي العلاقة.
- كما أن حل المعادلات والمتباينات الأسية يساعد العالم دائمًا من أجل التطور والنهوض من خلال استخدام الأساليب الجيدة التي تساعد بشكل كبير في حياتنا، كما تجعلنا نستطيع تناول علم الرياضيات الذي يعتمد على مجموعة من المعادلات والقواعد.
- فهو علم واسع يدخل فيه الكثير من الأمور المهمة بحياتنا، ويعرف علم الرياضيات بأنه العلم القائم على دراسة القياس والحساب.
- وقد عرف علم الرياضيات منذ وجود الإنسان على الأرض، وساعد في الوصول إلى العلم الذي يعطي لنا الحافز من أجل الحصول على أفضل الدرجات لفهم المادة العلمية التي تساهم في التعلم من الحياة، وقياس الظواهر الطبيعية، ومن خلال حديثنا عن علم الرياضيات سوف نقدم لكم حل المعادلات والمتباينات الأسية.
شاهد أيضًا: مراحل البحث العلمي وخطواته
تعريف المتباينات والمعادلات
- قبل البدء في شرح طريقة حل المعادلات والمتباينات الأسية.
- يجب أولًا تحديد الفرق بين المعادلات والمتباينات.
- فإن المعادلة في الرياضيات هي عبارة عن علاقة مساواة بين طرفين رياضيين تتكون من رموز رياضية.
- وذلك من خلال علامة التساوي (=)، على سبيل المثال تسمى المعادلة التالية: س+5=9، معادلة ذات مجهول واحد.
- أما المتراجحة أو المتباينة فهي علاقة رياضية بين طرفين تحتوي على أحد الرموز التالية: (>، ≤، ≥، >)، وهي لذلك تعبّر عن الاختلاف في قيمة عنصرين رياضيين، وبالتالي فإن المتباينة تعبر عن المقارنة بين طرفين، ولكن المعادلة هي عبارة عن مساواة بين عنصريين.
يمكننا تعريف المعادلة الأسية بأنها عبارة عن حالة خاصة من المعادلات، فإنها معادلة فيها الأُس يكون عبارة عن متغير، وليس ثابتًا، والصورة العامة لها هي كالآتي: أس = ب ص، حيث:
- س، وص: تكون الأُسس في المعادلة الأسية، وتتضمن المتغيرات التي عادة بإيجاد قيمها يكون حل المعادلة الأسية.
- حيث أن المعادلة الأسية تضم عادة متغيرًا واحدًا فقط.
- أ، ب: تعبر عن ثوابت، وهي عبارة عن الأساس في المعادلة الأسية.
طريقة حل المعادلات الأسية
معادلات أسيّة لها نفس الأساس:
هي المعادلة التي يكون فيها الأساس متساوي على طرفي إشارة التساوي، مثال على ذلك 4س = 4 9، ويتم الحل عن طريق استخدام القاعدة التي تنص على أنه عند تساوي الأساسات فإن الأسس تلقائيًا تتساوى، إذا كانت المعادلة على الصورة أس = ب ص، وكان أ=ب، فإن س=ص، فما هو ناتج حل المعادلة الأسية الآتية:5 3 س =5 7 س – 2؟
- بما أن الأساسات متساوية فإن الأسس بشكل تلقائي أيضًا تتساوى، وبالتالي: 3س=7س-2، وبالحل مثل المعادلات الخطية بطرح (3س) من الطرفين، يكون الناتج: 2 = 4س، ومنها: س= 1/2، ونستطيع التحقق من الحل من خلال تعويض قيمة س بطرفي المعادلة.
في بعض الحالات إذا كانت الأساسات ليست متساوية فإنه من الممكن إعادة كتابة المعادلة الأسية لتكون الأساسات متساوية فيها، وذلك إذا كانت مشتركة فيما بينها بعامل مشترك، والمثال التالي يوضّح ذلك:
- أوجد قيمة س في هذه المعادلة: 27 (4س + 1) = 9 (2س).
- لاحظنا في المثال السابق أن الأساسات غير متساوية، ولكن العدد 27، والعدد 9 يوجد بينهما عامل مشترك، وهو 3، حيث إن: 27 = 33 ،9 = 32.
- فإذا قمنا بتعويض هذه القيم في المعادلة الأسية فإن: (33)(4س + 1) = (32)(2س)، ومن خلال توزيع الأسس على القوس فإن: 3 (12 س + 3) = 3 (4س).
- بما أن الأساسات أصبحت الآن متساوية فإن الأسس أيضًا تتساوى كما يلي: 12س+3 =4س، وبحل المعادلة الخطية تكون النتيجة أن: 8س=-3، س = 3/8-.
تابع معنا: طريقة عمل بحث علمي | ما هي مراحل تطور البحث العلمي
المعادلات الأُسيّة التي ليس لها نفس الأساس:
هي المعادلة التي تكون أساساتها مختلفة، ويُصعب إعادة كتابتها حتى تصبح فيها الأساسات متساوية.
مثل 7س = 9، فلا يمكن هنا إعادة كتابة الأساس بشكل آخر لتصبح متساوية في النهاية.
ولذلك فإننا نحتاج إلى طريقة جديدة أخرى حتى نتمكن من حلها، والتي تكون من خلال استخدام اللوغاريتمات، وذلك كما يلي:
- إذا كانت المعادلة الأُسيّة على صورة مثل هذه: أس =جـ، فإنه من الممكن حلها بإدخال اللوغاريتم على الطرفين كما يلي: لو أس = لو جـ؛ حيث: أ، جـ: ثوابت، س: متغير.
- وفقًا للخصائص الخاصة باللوغاريتمات فإن: لو أس = س لو أ = لو جـ.
- وهنا يجب التنويه إلي أنه قد يختلف أساس اللوغاريتم مثل أن يكون العدد 10.
- أو قد يكون العدد النيبيري هـ فيصبح لوهـ، أو ما هو معروف باللوغاريتم الطبيعي، ولكي تتضح هذه الطريقة نقدم لكم المثال الآتي:
مثال: ما هو حل المعادلة الأسية الآتية: 4 (3 + س) =25 ؟
- من الصعب إعادة كتابة المعادلة السابقة لتكون فيها الأساسات متساوية، وبالتالي يتم إدخال اللوغاريتم على الطرفين مثلما يلي: لو 4(3+س)=لو25، ووفقًا لخاصية: لو أس = س لو أ فإن: (س+3) لو 4 = لو 25.
- نجعل المتغير س على طرف لوحده، وذلك من خلال قسمة الطرفين على لو4 لينتج أن: 3+س = لو25/ لو4، ثم بطرح العدد 3 من الطرفين ينتج أن: س= لو25/ لو4 – 3.
- مع استخدام الآلة الحاسبة فإن: لو25= 1.3979، لو4 = 0.602، وبعد تعويض هذه القيم يمكن حساب قيمة س كما يلي: س = 1.3979/0.602-3= 2.322 – 3= -0.678.
حل المعادلات الأسية التي تتضمن أعداداً صحيحة:
- في بعض الأحيان من الممكن أن تتضمن المعادلة الأسية أعداد صحيحة منفردة.
- تفصل إشارة طرح أو جمع بينها وبين التعابير الأسية.
- وطريقة حل المعادلة بعد التأكد من أن التعابير الأسية تقع بمفردها على طرف.
- والثوابت الأخرى التي ليس فوقها أسسًا تقع على طرف آخر، والمثال أدناه يوضّح ذلك.
مثال: ما هو حل المعادلة الأسية 3(س-5)-2 = 79؟
- لحل المعادلة أعلاه يجب أولًا طرح العدد 2 من كلا الطرفين لينتج أن: 3(س-5)= 79+2، 3(س-5)=81.
- بما أن العدد 81 هو عبارة 3×3×3×3؛ أي 34.
- فإنه من الممكن حل المعادلة من خلال توحيد الأساس.
- وذلك كما يلي: 3(س-5)=3 4، وبالتالي بما أن الأساسات أصبحت الآن متساوية فإن الأسس أيضًا تتساوى كالآتي: س-5 = 4، وبحل هذه المعادلة فإن س= 9
تابع معنا: بحث حول رحلات الإنسان إلى القمر
أنواع المعادلات
بعد شرح كيفية حل المعادلات والمتباينات الأسية يجب الآن تحديد أنواع المعادلات الجبرية.
والتي يتم تقسيمها حسب عناصرها ومكوناتها إلى ما يأتي:
- المعادلات الحدودية: معادلة تساوي بين متعددة حدود ما، ومتعددة حدود أخرى.
- المعادلات الجبرية، علاقة مساواة بين عنصرين جبريين يحتوي أحدهما أو كلاهما على متغيرًا واحدًا على الأقل.
- والمعادلات الخطية هي معادلة جبرية بسيطة تسمى معادلة من الدرجة الأولى.
- المعادلات المتسامية: المعادلة التي تحتوي على دالة متسامية أي دالة مثلثية أو أسية أو معكوساتها.
- والمعادلات التفاضلية: وهي المعادلات التي تربط أحد الدوال بمشتقاتها.
- المعادلات الديفونتية: سميت بذلك نسبةً إلى العالم اليوناني ديوفنطس.
- وهي معادلة حدودية مكونة من متغيرات متعددة يتم حلها بأعداد صحيحة أو يبرهن على استحالة الحل.
- والمعادلات الدالية: وهي المعادلات التي يكون فيها المجهول أو المجاهيل دوالًا بدلًا من أن تكون مجرد متغيرات.
- المعادلات التكاملية: هي معادلة تضم دالة غير مُعرفة بجانب إشارة التكامل.
أنواع المتباينات
المتباينات مقسمة بين معقدة وبسيطة، ومنها ما يسمى بالتفاوتات المشهورة في علم الرياضيات، ونذكر منها ما يلي:
المتباينة المثلثية: وتعني أن طول أي ضلع من أضلاع المثلث يكون قطعًا أصغر من مجموع طولي الضلعين الآخرين، وهو قطعًا أكبر من الفارق بينهما.
- عدم المساواة Cauchy-Schwarz، الذي سمي بذلك نسبةً إلى اسم العالم الروسي شوارتز والفرنسي كوشي.
- فيما يتعلق بعلم المثلثات والقواعد الإقليدية
- عدم المساواة في الوظائف للعالم الروسي أندري ماركوف.
- متباينة برنولي السويسرية للدالة الأسية.
تعتبر المتباينات والمعادلات فرع هام جدًا من فروع علم الجبر، وله استخدامات متعددة وقد قدمنا لكم بحث عن حل المعادلات والمتباينات الاسية وأنواعها كاملة، ووضحنا أن لها أشكال مختلفة ومتعددة، نتمنى أن ينال المقال إعجاب كل المهتمين بعلم الرياضيات.