الشكل الناتج من دوران المستطيل
الشكل الناتج من دوران المستطيل، الأسطوانة هي مادة صلبة مغلقة لها قاعدتان متوازيتان (عادة دائرية) متصلة بسطح منحني، حيث أنها هي مادة هندسية شائعة جداً في الحياة اليومية، مثل علبة الحساء، إذا انفصلت عن ذلك فوجدت أن له طرفان، يطلق عليهما قواعد يكونان دائريين، القواعد دائما متطابقة ومتوازية مع بعضها البعض.
محتويات المقال
ما هي الاسطوانة؟
- من الجدير بالذكر التأكيد على أنه إذا كنت تريد “فك الاسطوانة” ستجد أن الجانب مستطيل بالفعل عند تسويته، ارتفاع الاسطوانة هو المسافة العمودية بين القواعد. من المهم استخدام الارتفاع العمودي (أو “الارتفاع”) عند حساب حجم الاسطوانة المائلة.
- عندما يكون القاعدتان فوق بعضهما بعضاً تماماً ويكون المحور زوايا قائمة على القاعدة، فإن هذا يسمى “الاسطوانة الصحيحة”، إذا تم إزاحة قاعدة واحدة جانبية فإن المحور ليس في الزوايا الصحيحة للقواعد وتسمى النتيجة أسطوانة مائلة، القواعد وإن لم تكن مباشرة على بعضها البعض، لا تزال موازية.
- لكن لابد من التأكيد على أن المنشور هو مادة صلبة ذات قواعد مضلعة والجوانب سطحية مسطحة، بالمعنى الدقيق للكلمة الاسطوانة ليست هي نفسها المنشور، ومع ذلك فهي متشابهة للغاية.
- في المنشور تكون القواعد مضلعات منتظمة، يبدأ المنشور في الاقتراب من كونه أسطوانة عندما يكون عدد الجوانب كبيراً.
شاهد أيضًا: بحث عن المربع والمعين والمستطيل
ما الشكل الناتج من دوران المستطيل؟
- بالتأكيد الشكل الناتج عن دوران المستطيل هو الأسطوانة والتي هي عبارة عن شكل ثلاثي الأبعاد مع شكلين دائريين في أي من الطرفين وخطين متوازيين يربطان الطرفان المستديران القواعد هي دائمًا موازية مطابقة لبعضها البعض.
- لابد من معرفة أن الأسطوانة تسمى باللغة الإنجليزية: The cylinder، هي عبارة عن مجسم ثلاثي الأبعاد، يحتوي على قاعدتين إحداهما علوية وأخرى سفلية، من المهم معرفة أن كل منهما شكلاً دائرياً، وما يميز هاتين القاعدتين هو تقابلهما وتطابقهما.
- من الجدير بالذكر أنه ينتج الشكل الأسطواني من خلال التفاف دوران مستطيل حول أحد جوانبه دوره بشكل كامل.
- أما بالنسبة للشكل الأسطواني له مجموعة من المميزات، التي منها هو أنه يشتمل على جانب وحيد على شكل منحنى، ومن الجدير بالذكر أن له قاعدة تكون مسطحة الشكل.
انواع الاسطوانات
هناك نوعان من الاسطوانات:
1.اسطوانة دائرية صحيحة
عندما يكون قاعدتا الأسطوانة فوق بعضهما البعض في الموضع المحدد ويكون المحور في الزاوية اليمنى للقاعدة، يطلق عليه الاسطوانة هي الاسطوانة الصحيحة.
2. اسطوانة منحرفة (مائلة)
عندما تكون إحدى قواعد الأسطوانة جانبية ولم يكن المحور زاوية صحيحة للقاعدة، فهي عبارة عن أسطوانة مائلة.
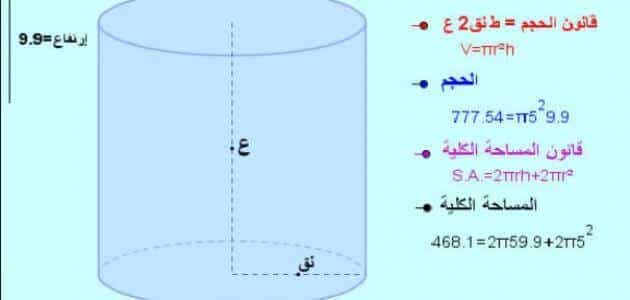
حساب مساحة الأسطوانة الجانبية والكلية
تعتبر المساحة الجانبية للأسطوانة هي: حاصل ضرب محيط الدائرة في ارتفاع الأسطوانة، أي 2 ×π× نصف القطر× ارتفاع الأسطوانة.
من الجدير بالذكر أنه لحساب مساحة كل قاعدة من قاعدتي الاسطوانة لوحدها يتم ذلك من خلال قانون مساحة الدائرة وهي: مساحة الدائرة=π× (نصف القطر) ².
المساحة الكلية للأسطوانة=المساحة الجانبية +مجموع مساحة القاعدتين.
المساحة الجانبية=محيط الدائرة ×ارتفاع الأسطوانة.
المساحة الجانبية = 2×نق×π×ع.
مساحة القاعدة الواحدة =π× (نق)².
المساحة الكلية للأسطوانة = (2 نقπ ع) + (2 نق² π).
من خلال إخراج العوامل المشتركة تصبح: المساحة الكلية للأسطوانة = 2× نق× π (ع +نق).
خصائص الاسطوانة
- من المهم التأكيد على أن الأسطوانة تشتمل على جانب منحنى واحد فقط.
- من المعروف أن الاسطوانة لها طرفان مسطحان متطابقان دائريان أو بيضاويان.
- القواعد دائما متطابقة ومتوازية.
- يشبه المنشور لأنه يحتوي على نفس المقطع العرضي في كل مكان.
- لابد من معرفة الأسطوانة لها قاعدتان مسطحتان شكلهما دائري.
- من المعروف أن الاسطوانة لها واجهة واحدة، تنتج من دوران المستطيل حول أحد أضلاعه.
أمثلة على حساب المساحة الكلية والجانبية للأسطوانة
المثال الأول:
قم بإيجاد المساحة الجانبية والكلية أسطوانة دائرية قائمة، إذا علمت أن نصف قطر قاعدتها الدائرية يساوي 7 م، أما ارتفاعها فيساوي 10م.
الحل:
- المساحة الكلية للأسطوانة = المساحة الجانبية +مجموع مساحة القاعدتين.
- المساحة الجانبية = 2×نق×π×ع.
- من خلال تعويض قيمة الارتفاع= 10، ونق=7، في القانون، تكون:
- المساحة الجانبية = 2×7×π×10.
- المساحة الجانبية للأسطوانة = 140 π م².
- مساحة القاعدتين = 2×مساحة القاعدة الواحدة.
- مساحة القاعدتين = 2× نق²×π.
- مساحة القاعدتين = 2×7×7×π.
- مساحة القاعدتين = 98 π م².
- أما بالنسبة للمساحة الكلية للأسطوانة = 140 π 98 +π
- إذن: المساحة الكلية للأسطوانة = 238 πم².
المثال الثاني:
قم بإيجاد المساحة الجانبية والكلية أسطوانة دائرية قائمة، إذا علمت أن نصف قطر قاعدته الدائرية يساوي 4 دسم، أما ارتفاعها فيساوي 12 دسم.
الحل:
- المساحة الكلية للأسطوانة = المساحة الجانبية +مجموع مساحة القاعدتين.
- المساحة الجانبية = 2×نق×π×ع.
- من خلال بتعويض قيمة الارتفاع= 12، ونق=4، في القانون، تكون:
- المساحة الجانبية = 2×4×π×12.
- المساحة الجانبية للأسطوانة = 96 π دسم².
- مساحة القاعدتين= 2×مساحة القاعدة الواحدة.
- مساحة القاعدتين = 2× نق²×π.
- مساحة القاعدتين = 2×4×4×π.
- مساحة القاعدتين = 32 π دسم².
- المساحة الكلية للأسطوانة = 96 π 32 +π.
- وبالتالي تكون المساحة الكلية للأسطوانة = 128 π دسم².
شاهد أيضًا: قانون مساحة المستطيل ومحيطه بالتفصيل
حساب حجم الاسطوانة
من الجدير بالذكر أنه يتم حساب حجم أي شكل أسطواني من خلال ضرب مساحة قاعدة الاسطوانة في الارتفاع، كما أنه معروف أن القاعدة تمثل دائرة، يتم التوصل إلى أن مساحة قاعدة الأسطوانة تساوي مساحة الدائرة، والتي هي:
مساحة الدائرة= π× (نصف القطر) ²، وبالتالي فإن حجم الأسطوانة يساوي: (حجم الاسطوانة = مساحة قاعدة الأسطوانة × ارتفاع الأسطوانة).
كما أنه لابد من معرفة أن مساحة قاعدة الأسطوانة = مساحة الدائرة.
مساحة قاعدة الأسطوانة = π× (نق)².
حجم الأسطوانة = π× نق²×ع.
من الجدير بالذكر أن: نق: نصف قطر الدائرة أو القطر مقسوماً على العدد 2.
أما بالنسبة ع: ارتفاع الأسطوانة.
استخدامات الاسطوانة
- أسهل في التصنيع.
- يكون شكله أكثر ثباتاً ضد الضغط الداخلي للسوائل أو الغاز مقارنة بالحاويات المكعبة.
- أكثر ملاءمة في ملء السوائل أو المواد الصلبة الحبيبية بالمقارنة مع الحاويات الكروية.
- يبقى أكثر استقراراً على الأرض مقارنةً بالحاويات الكروية.
- أخف وزناً وأرخص وأكثر اقتصادًا وأكثر كفاءة.
- من الممكن أن يتم استخدام الاسطوانات في مضخات المياه، حيث أنه من المعروف أن مضخة المياه تتكون من مجسم أسطواني يستخدم لضخ السائل إلى الخارج بقوة دفع كبيرة.
- من الاستخدامات أيضاً الشكل الأسطواني تكون في المنسوجات، من المهم التأكيد أنه تتشكل الآلة الخاصة بتمشيط المنسوجات أو ألياف الملابس والخيوط المكونة للمنسوجات والملابس من شكل مجسم أسطواني.
- في علم الآثار، الكثير من الآثار الخاصة بالشعوب القديمة والبابليون والآشوريون وغيرها من الشعوب، تحتوي على مجسمات عدة ومنها المجسمات الأسطوانية مثال على ذلك البراميل والأعمدة المنقوشة والمنحوتة.
- قد يتم استخدام الشكل الاسطواني في المطابع، من الجدير بالذكر أن تلك المجسمات والأشكال تكون في شكل أسطواني، حيث أن الآلة المنحنية التي يدور حولها الورق ليتم طباعته هي على شكل أسطوانة.
أمثلة على الشكل الأسطواني
- قنينة المياه.
- أنبوب اختبار.
- اسطوانات محرك السيارة.
- أنابيب النحاس للمياه.
- الأنابيب البلاستيكية.
- أنابيب الصلب.
- شمعة.
- بطارية مزدوجة.
- بطارية ثلاثية.
- السيجارة.
- لفة ورق التواليت.
- لفة من المناشف الورقية.
- قطعة طبشور.
- حامل قلم رصاص.
شاهد أيضًا: بحث عن الاشكال الرباعية والمجسمات
في نهاية رحلتنا عن الشكل الناتج من دوران المستطيل ، يكون تم التعرف على أن الشكل الناتج عن دوران المستطيل هو الاسطوانة وتم التوصل إلى كيفية إيجاد مساحة وحجمه ومن أهم استخداماته.